深入解析 RNS-CKKS 中的高效密钥切换：Hybrid Approach 原理与推导

在全同态加密（FHE）的硬件加速与软件库实现（如 Lattigo, OpenFHE）中，密钥切换（Key-Switching / Relinearization） 往往是性能的最主要瓶颈。

在 RNS-CKKS 方案中，如何高效地处理密钥切换一直是一个核心难题。从最早的两种朴素实现（Type I 和 Type II），发展到如今被广泛采用的 Hybrid Approach（混合方法），其背后的数学直觉与工程权衡非常精彩。

本文将详细剖析论文《Efficient Bootstrapping for Approximate Homomorphic Encryption with Non-Sparse Keys》中 Hybrid Approach 的数学原理，给出严谨的正确性证明，并对比其与传统方法的优劣，特别适合正在进行 FHE GPU/ASIC 加速器开发的开发者阅读。

1. 背景：Key-Switching 的核心矛盾

在 CKKS 中，密文乘法后会得到一个三元密文 $(c_0, c_1, c_2)$ ，其解密形式包含 $s^2$ 项： $c_0 + c_1 s + c_2 s^2$ 。为了让密文继续保持“由同一个秘密钥 $s$ 解密”的形态，我们需要将其重线性化/密钥切换回二元密文 $(d_0, d_1)$ ，使得 $d_0 + d_1 s \approx c_0 + c_1 s + c_2 s^2$ 。这一过程使用评估密钥（Switching Key / Relinearization Key） $\text{swk}_{s^2 \rightarrow s}$ ，其计算核心可以理解为：对 $c_2$ （以及其分解后的 digits）与 $\text{swk}$ 做内积累加，从而“吸收”掉 $s^2$ 项。

如果将其误实现为“直接同态计算密文与秘密钥的乘法”，会引入不可控的噪声放大并破坏正确性。工程实现中，为了在 RNS 下稳定地完成上述内积与后续的 ModDown，通常需要引入辅助模数 $P$ 。

在 Hybrid Approach 出现之前，存在两种极端的处理流派：

Type I (Bit/Digit Decomposition)：将密文切得非常碎（例如按 RNS 素数切分）。
- 优点：不需要辅助模数 $P$ ，或 $P$ 很小。
- 缺点：计算量极大（需要做 $L$ 次 NTT 和乘法），存储开销大。
Type II (Modulus Raising)：不切分，直接引入一个巨大的辅助模数 $P$ $P$ ( $P \approx Q$ $P \approx Q$ )。
- 优点：计算次数最少（只需 1 次乘法）。
- 缺点：参数爆炸。由于 $P \approx Q$ ，总模数 $PQ$ 翻倍，迫使多项式度数 $N$ 升级（例如从 $2^{15}$ 升至 $2^{16}$ ），导致整体性能雪崩。

Hybrid Approach 的诞生，就是为了在“计算复杂度”和“参数大小”之间寻找一个最佳甜点（Sweet Spot）。

2. Hybrid Approach 的核心思想

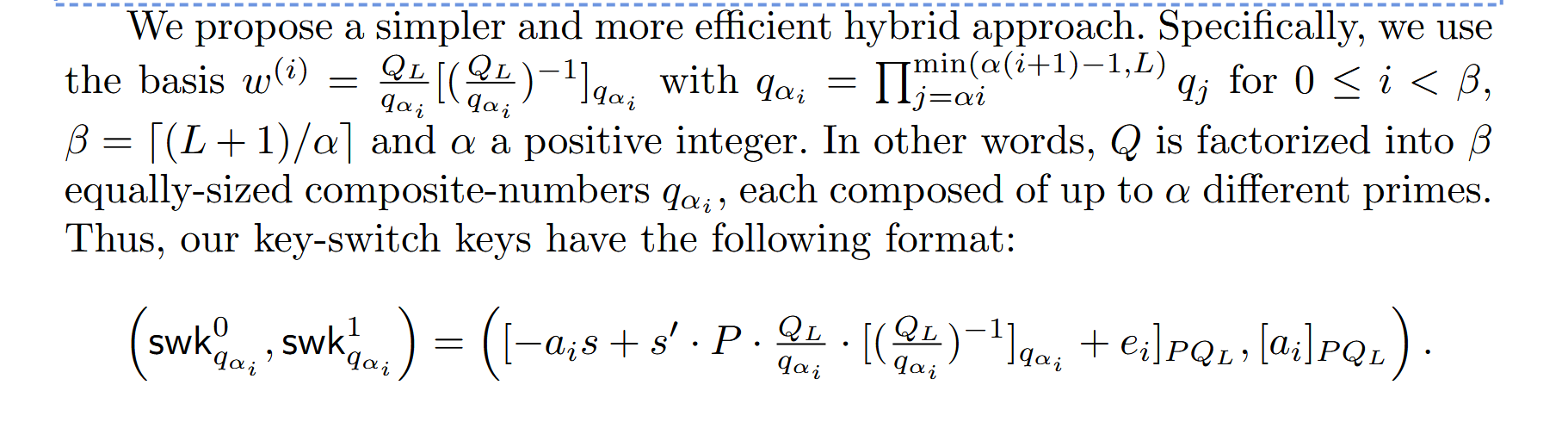
Hybrid Approach 引入了一个分解因子 $dnum$ （在部分文献中记为 $\beta$ ）。它将模数链 $Q$ 分解为 $dnum$ 个分块（Digits）。

适度的分解：我们不像 Type I 那样切成几十块，也不像 Type II 那样完全不切，而是切成 $2 \sim 4$ 块。
适度的 $P$ ：由于进行了分解，辅助模数 $P$ 只需要大于分块的大小即可（即 $P \approx Q / dnum$ ）。这成功避免了总模数 $PQ$ 的过度膨胀。

2.1 密钥结构

为了支持这种分解，我们利用 中国剩余定理（CRT） 构造了一组特殊的基底 $w^{(i)}$ 。 Key-Switching Key ( $swk$ ) 被定义为 $dnum$ 个密文的集合：

$\mathbf{swk}^{(i)} = \left( -a_i s + e_i + P \cdot w^{(i)} \cdot s', \quad a_i \right) \pmod{PQ}$

其中 $w^{(i)}$ 是针对第 $i$ 个分块的 CRT 基底。

3. 数学原理与正确性证明 (详细推导)

很多开发者对 Hybrid Approach 的困惑在于：为什么把密文切开再乘，最后还能加回去，且噪声还能被消除？ 下面我们通过严谨的代数推导来证明其正确性。

3.1 预备定义

$R_Q$ ：模 $Q$ 的多项式环。
分解：将 $c \in R_Q$ 分解为 $dnum$ 个分量 $c^{(i)}$ ，其中 $c^{(i)}$ 仅在第 $i$ 个分块的素数基中有值。
CRT 基底 $w^{(i)}$ 的定义： $w^{(i)} = \frac{Q}{q_{\alpha_i}} \left[ \left( \frac{Q}{q_{\alpha_i}} \right)^{-1} \right]_{q_{\alpha_i}}$ 关键性质：CRT 重构性质保证了 $\sum_{i} c^{(i)} w^{(i)} \equiv c \pmod Q$ 。即在整数环上，存在多项式 $k$ ，使得： $\sum_{i=0}^{dnum-1} c^{(i)} w^{(i)} = c + k \cdot Q$

3.2 推导过程

算法的核心步骤包含：扩展、内积、ModDown。

步骤 1：内积运算 (Inner Product)

我们在模 $PQ$ 下计算密文分量与密钥的内积： $\text{C}_{tmp} = \sum_{i=0}^{dnum-1} c^{(i)}_{extended} \cdot \mathbf{swk}^{(i)} \pmod{PQ}$

注意：这里的 $c^{(i)}_{extended}$ 指的是通过 BConv 将 $c^{(i)}$ 从其原本的小素数基扩展到整个 $PQ$ 模数链后的结果。

让我们观察解密后的相位 (Phase)： $\begin{aligned} \text{Phase}(\text{C}_{tmp}) &= \sum_{i} c^{(i)} \cdot \text{Phase}(\mathbf{swk}^{(i)}) \\ &= \sum_{i} c^{(i)} \cdot \left( P \cdot w^{(i)} \cdot s' + e_i \right) \pmod{PQ} \end{aligned}$

步骤 2：提取公因式与 CRT 重构

将上式展开： $\text{Phase}(\text{C}_{tmp}) = P \cdot s' \cdot \underbrace{\left( \sum_{i} c^{(i)} w^{(i)} \right)}_{\text{CRT重构}} + \underbrace{\sum_{i} c^{(i)} e_i}_{\text{噪声项 } E_{total}} \pmod{PQ}$

利用 3.1 中的 CRT 关键性质 $\sum c^{(i)} w^{(i)} = c + kQ$ ，代入上式： $\begin{aligned} \text{Phase}(\text{C}_{tmp}) &= P \cdot s' \cdot (c + k \cdot Q) + E_{total} \pmod{PQ} \\ &= P \cdot c \cdot s' + \mathbf{P \cdot k \cdot Q \cdot s'} + E_{total} \pmod{PQ} \end{aligned}$

步骤 3：模数 $PQ$ 的魔法 (消除 kQ)

请注意加粗项 $\mathbf{P \cdot k \cdot Q \cdot s'}$ 。因为该项包含因子 $P$ 和 $Q$ ，它必然是 $PQ$ 的倍数。在 $\pmod{PQ}$ 的环中，该项恒等于 0。

因此，内积的结果简化为： $\text{Phase}(\text{C}_{tmp}) \equiv P \cdot c \cdot s' + E_{total} \pmod{PQ}$

步骤 4：Modulus Down (除以 P)

最后一步是 RNS 下的 Modulus Down，其数学意义是乘以 $P^{-1}$ ： $\text{Result} \approx \text{C}_{tmp} \cdot P^{-1} \pmod Q$

解密结果为： $\begin{aligned} \text{Phase}_{final} &\approx P^{-1} \cdot (P \cdot c \cdot s' + E_{total}) \\ &= c \cdot s' + \frac{E_{total}}{P} \end{aligned}$

结论：

正确性：我们成功还原了 $c \cdot s'$ 。
噪声控制：总噪声 $E_{total}$ 被巨大的辅助模数 $P$ 除掉了。只要 $P$ 足够大（ $P \approx Q/dnum$ ），剩余噪声 $\frac{E_{total}}{P}$ 就可忽略不计。

4. 深度剖析：Algorithm 3 的数据流向与 RNS 陷阱

在阅读相关文献（如 SHARP 论文或 Lattigo 源码）时，Algorithm 3 的第一行往往是最容易产生误解的地方。为了确保在 GPU/ASIC 上正确实现，需要结合 RNS 的算术特性，对数据流向进行严格的剖析。

4.1 核心结论：全模数扩展

观察算法第 1 行的公式：

$\mathbf{d} \leftarrow [[c]_{q_{\alpha_0 \le i < \beta}}]_{PQ_\ell}$

这里表达了一个至关重要的实现细节：第一步生成的向量 $\mathbf{d}$ ，其每一个分量都必须被扩展到完整的模数链 $PQ_\ell$ 上，而不仅仅是 $P \cup q_{\alpha}$ 。

为什么？这是由 RNS 的乘法铁律 决定的：两个多项式要相乘，它们必须定义在“完全相同”的 RNS 基（素数集合）上。

4.2 详细原理解析

让我们拆解这一过程：

内层操作（分解） $[c]_{q_{\alpha_i}}$ ：

把密文 $c$ 切成 $\beta$ 个小块（Digits）。第 $i$ 个小块 $c^{(i)}$ 初始时刻只存在于它自己的素数基 $q_{\alpha_i}$ 中。
外层操作（扩展） $[\cdot]_{PQ_\ell}$ ：

这是完全扩展 (Full BConv)。需要把每一个小块 $c^{(i)}$ ，通过 BConv 扩展到整个当前的模数系统 $PQ_\ell$ （即 $Q$ 的所有素数 + 辅助模数 $P$ ）。

为什么要扩展到整个 $PQ_\ell$ ？（而不是只扩展到 P）

这对应了算法 Line 2 的点积操作：

$(a, b) \leftarrow (\langle \mathbf{d}, \mathbf{swk}^0 \rangle, \dots)$

展开来看，其本质是求和：

$\text{Result} = c^{(0)}_{\text{extended}} \cdot swk^{(0)} + c^{(1)}_{\text{extended}} \cdot swk^{(1)} + \dots$

请注意 Key ( $swk$ ) 的形态：

$swk^{(i)}$ 是预计算好的密钥，它必须存储在所有模数 ( $PQ_\ell$ ) 上。因为它包含 $s' \cdot P$ 这种项，且为了后续能正确 ModDown 回 $Q$ ，它必须在整个 $Q$ 上也有定义。
RNS 对齐限制：在计算设备上执行 Mult(A, B) 时，如果 A 只有 3 个 limb (mod $q_0, q_1, q_2$ )，而 B 有 5 个 limb (mod $q_0 \dots q_4$ )，是无法进行点乘的。数据必须在维度上完全对齐。

因此，虽然 $c^{(0)}$ 原本只在 $q_{\alpha_0}$ 上有值，但为了和“全尺寸”的 $swk^{(0)}$ 相乘，它必须被 BConv 投影到 $swk^{(0)}$ 所在的所有素数上。

4.3 修正后的完整数据流 (Step-by-Step)

假设 $Q = \{q_0, q_1, q_2, q_3\}$ ， $P = \{p_0\}$ ， $dnum=2$ 。

Digit 0 是 $\{q_0, q_1\}$ ，Digit 1 是 $\{q_2, q_3\}$ 。

Step 1: 分解与全扩展 (Algorithm 3, Line 1)
- 从密文 $c$ 中切出第一块 $c^{(0)}$ （在 $q_0, q_1$ 上）。
- 关键修正：需要计算 $c^{(0)}$ 在 $\{q_2, q_3, p_0\}$ 上的投影。
  - 误区提示： $c^{(0)}$ 不是在 $\{q_2, q_3\}$ 上填 0！
  - 正确做法： $c^{(0)}$ 是一个整数多项式，它在 mod $q_2$ 下有具体的非零值。需要通过 INTT (在 $q_0, q_1$ ) -> BConv -> NTT (在 $q_2, q_3, p_0$ ) 算出来。
- 最终，得到一个“胖”的 $c^{(0)}_{full}$ ，它在 $\{q_0, q_1, q_2, q_3, p_0\}$ 上都有值。
- 同理处理 $c^{(1)}$ ，得到“胖”的 $c^{(1)}_{full}$ 。
Step 2: 内积 (Line 2)
- 计算 $c^{(0)}_{full} \cdot swk^{(0)}$ （全模数链乘法）。
- 计算 $c^{(1)}_{full} \cdot swk^{(1)}$ （全模数链乘法）。
- 相加得到结果 $\text{Tmp}$ （在 $PQ_\ell$ 上）。
Step 3: ModDown (Line 3)
- 现在 $\text{Tmp}$ 在 $PQ_\ell$ 上。
- 执行标准的 ModDown 流程：取 $P$ 分量 $\to$ 扩展回 $Q$ $\to$ 相减 $\to$ 乘 $P^{-1}$ $\to$ 丢弃 $P$ 。

4.4 理论直觉与 RNS 实现的差异

为什么容易产生“填 0”或“只扩展到 P”的误解？这是因为混淆了 CRT 基底的理论性质 和 RNS 的具体实现。

理论上：如果看的是 $c = \sum c^{(i)} w^{(i)}$ 这个公式，CRT 基底 $w^{(i)}$ 在其他 $q_j$ （非当前 digit）下确实是 $0 \pmod {q_j}$ 。
实际上：Algorithm 3 不是直接构造 $w^{(i)}$ 。它是把 $c^{(i)}$ 当作一个独立的数，去乘 $swk^{(i)}$ 。而 $swk^{(i)}$ 内部隐含了 $w^{(i)}$ 。为了执行这个乘法，数据必须对齐到全模数。

4.5 针对 GPU 实现的建议

基于上述分析，在 28-bit GPU 实现中，应当构建以下三个核心 Kernel：

Kernel 1 (Full BConv): 实现一个能够将 $dnum$ 个小块，分别广播/扩展到整个模数链 $PQ$ 的 Kernel。这会是计算密集度很高的一步，复杂度为 $O(dnum \cdot L \cdot N)$ 。
Kernel 2 (MultAcc): 在全模数链 $PQ$ 上执行点积累加。
Kernel 3 (ModDown): 再次调用 BConv 把 $P$ 上的结果投影回 $Q$ ，然后做减法。

5. 对比与权衡 (Trade-off)

为什么 Hybrid Approach 能够胜出？以下是三种方案的详细对比：

特性	Type I (Bit Decomposition)	Type II (Modulus Raising)	Hybrid Approach (Sweet Spot)
分解数量 ( $dnum$ )	$L$ (约 20~60)	$1$	2 ~ 4
辅助模数 $P$ 大小	不需要或很小	$P \approx Q$ (巨大)	$P \approx Q / dnum$ (适中)
总模数 $PQ$	$\approx Q$	$\approx Q^2$	$\approx Q \cdot Q^{1/dnum}$
密钥存储 (swk)	$L$ 个	1 个	$dnum$ 个
计算复杂度	极高 ( $L$ 次乘法)	低 (1 次大乘法)	中等 ( $dnum$ 次乘法)
参数安全性 $N$	优秀	差 (易导致 N 翻倍)	优秀 (保持小 N)

分析结论

为什么不用 Type II？ 虽然 Type II 只需要存 1 个 Key，算 1 次乘法，看似最快。但由于 $P \approx Q$ ，导致总模数 $PQ$ 极大。为了满足同态加密的安全性（128-bit Security），更大的模数要求更大的多项式度数 $N$ 。一旦 $N$ 从 $2^{15}$ 被迫增加到 $2^{16}$ ，计算延迟会增加 2-4 倍，内存占用翻倍。这是得不偿失的。
为什么 Hybrid 是最优解？ Hybrid 通过设置 $dnum \approx 3$ ，使得 $P$ 只有 $Q$ 的三分之一大小。这样 $PQ$ 的总大小通常能维持在当前 $N$ 的安全范围内。虽然我们需要存储 3 个 Key，多做几次 BConv，但相比于 $N$ 翻倍带来的性能损耗，这些开销是完全可以接受的。
显存带宽优化 针对 GPU 实现，存储 $dnum$ 个 Key 可能会占用大量带宽。SHARP 论文和现代库建议使用 PRNG (伪随机数生成器)：
- $swk = (-a \cdot s + \dots, a)$ 。
- 其中多项式 $a$ 是随机的。我们在显存中只存一个 32字节的 Seed。
- 在计算时，GPU 动态生成 $a$ ，从而将带宽占用减半。

6. 总结

Hybrid Approach 是 RNS-CKKS 密钥切换技术的集大成者。它利用 CRT 的代数性质，巧妙地化解了噪声与效率的矛盾。

对于硬件开发者而言，理解其背后的 “扩展 -> 内积 -> 模约减” 这一 RNS 数据流至关重要。正确实现 Hybrid Approach，并配合 $dnum$ 的参数调优，是实现高性能 FHE 加速器的关键一步。

密钥切换 - hybrid Approach