推荐阅读:本文是原始的深度问答记录(Q&A)。如果您想阅读经过整理、结构更清晰的技术博客版本,请访问:深度解析:CKKS 同态加密中的多精度乘法优化 (HMPM)
这篇文章的后续思考:第二篇文章
前言
本文记录了与 Gemini 3 关于论文《Homomorphic Multiple Precision Multiplication for CKKS and Reduced Modulus Consumption》的深度对话。论文作者:Jung Hee Cheon, Wonhee Cho, Jaehyung Kim, 和 Damien Stehlé。
论文核心内容概述
核心痛点与目标
- 痛点:现有的 CKKS 方案在每次乘法(Rescaling)中会消耗大量的密文模数。当模数耗尽时,需要昂贵的自举(Bootstrapping)操作。
- 目标:通过一种新的乘法算法(),在保持精度的同时,将模数消耗减少近一半。
核心技术创新
- 同态欧几里得除法 (Homomorphic Euclidean Division):论文提出了一种将密文分解为”商”(高位部分)和”余数”(低位部分)的方法。
- 对表示法 (Pair Representation):将一个标准 CKKS 密文 分解为一对密文 。
- 算法:针对分解后的密文对执行同态乘法。它包含三个修改后的步骤:
- :类似于双精度乘法,但舍弃了影响最小的项(低位 低位),从而节省模数。
- :对分解后的部分进行重线性化。
- :修改后的重缩放(Rescaling)操作。
扩展与应用
- Double-CKKS & Tuple-CKKS:将该方法扩展到 的情况(即 ),可以进一步降低模数消耗,实现同态多精度算术。
- 优势:
- 增加同态容量:在相同的参数下,可以执行更多层的乘法。
- 提高精度:可以使用较小的参数(如环维数 )来实现高精度计算(例如 100-bit scaling factor)。
- 效率提升:通过减半模数,可以减半环维数,从而减少密文大小和计算延迟。
实验结果
- 论文展示了在 时,Double-CKKS 可以支持 18 层乘法,而标准 CKKS 仅支持 13 层。
- 在高精度场景下, 在计算速度、密文大小和密钥大小方面均优于标准方法。
第一部分:基础概念与动机
Q1: RNS-CKKS 与方案兼容性
问题:这个方案不是基于 RNS-CKKS 的吗?为什么说乘法比特数越大,模数消耗越多?Euclidean division 是什么?为什么密文的低位是在 这个数域中?
回答:
1.1 这个方案是基于 RNS-CKKS 的
是的,这个方案完全兼容并且是基于 RNS-CKKS 实现的。
虽然在论文的理论部分(Section 1 到 4),为了公式推导的简洁性,作者通常使用一个大的整数模数 来描述(比如写成 ),这在密码学论文中很常见,为了避免符号过于复杂。
但在实验部分(Section 6) 和 具体实现讨论(Section 4.2 Modulus consumption) 中,作者明确指出:
- 代码是基于 HEaaN 库 开发的(这是一个经典的 RNS-CKKS 库)。
- 实现依赖于 RNS arithmetic。
- 特别是对于新引入的模数 ,在 RNS 系统中,它通常被选为 RNS 质数基中的一个或多个质数的乘积。
所以,理论上讲它是通用的,但工程上它就是为了 RNS-CKKS 设计的优化。
1.2 为什么说”乘法比特数越大,模数消耗越多”?
这句话的逻辑链条如下:
-
精度与缩放因子(Scaling Factor )的关系:在 CKKS 中,为了支持小数运算并保持精度,我们把消息 放大 倍,变成整数形式存储。如果你想要处理更大比特数(即更高精度或更大数值范围)的乘数,你需要更大的缩放因子 来保证在噪声影响下依然能正确解码有效位。
-
乘法带来的膨胀:当你计算两个密文相乘 时,底层的消息变成了 。此时缩放因子变成了 。
-
Rescaling(重缩放)消耗模数:为了让后续计算能继续进行,必须把缩放因子从 降回 。这是通过 Rescaling 操作完成的,本质上是把密文除以 。而在 CKKS 中,除以 是通过模数切换(Modulus Switching) 实现的:模数从 变成了 。
结论:
- 乘数比特数大 需要更大的缩放因子 。
- 越大 每次 Rescaling 消耗掉的模数( bits)就越多。
- 因此,为了支持大数(高精度)乘法,传统的 CKKS 会迅速耗尽模数,导致能支持的电路深度变浅。这正是论文想要解决的痛点。
1.3 Euclidean division 是什么?
Euclidean division 就是我们在小学数学里学的带余除法(欧几里得除法)。
对于任意整数 (被除数) 和 (除数,且 ),存在唯一的整数 (商) 和 (余数),满足: 其中 。
在论文中的应用:
论文把这个概念应用到了密文(或者说是多项式的系数)上。作者想把一个大密文 分解成两部分。选定一个除数 (或者文中的 ),那么密文就可以表示为:
- 是商(对应高位,High part)。
- 是余数(对应低位,Low part)。
这就像把数字 按照 分解:。 是高位, 是低位。论文正是利用这种分解,把一个大精度的乘法拆成了几个小精度的乘法来做。
1.4 关于 1.1 节截图中的两个问题
问题 A:为什么密文的低位 是在 这个数域中(而不是 )?
这里 指的是整数多项式环 。
- 原因: 是 除以 的余数。
- 根据欧几里得除法的定义,余数的系数绝对值一定小于除数的一半,即 。
- 文中假设模数 远大于 ()。
- 结论: 因为 的系数非常小(远没有达到模数 的边界),它在模 的意义下和在整数 的意义下是完全一样的,不会发生取模回绕(Wrap-around)。所以作者说它可以被视为直接在 (整数域)中,这强调了它是精确的数值,没有模数噪声。
问题 B:为什么解密后的误差项满足 ?
这是一个通过线性关系推导出来的结果,目的是为了保证总和不变。
- 分解关系: 密文被分解为 。
- 解密即线性运算: 解密函数 是线性的。所以:
- 定义误差:
- 设理想的商是 ,实际解密出的是 ( 是商的误差)。
- 设理想的余数是 ,实际解密出的是 。
- 我们知道原消息 。
- 代入等式: 消去 ,得: 移项得:
- 对应定义: 作者把 写成了 的形式。 对比上面推导出的式子:。 所以:。
直观理解: 如果你在计算“商”(高位)的时候多算了 ,那么因为商是被乘了 的,所以你实际上多算了 。为了让总数保持不变(还是原来的 ),你的“余数”(低位)就必须相应地少算 来把这个误差抵消掉。
这就是文中提到的 “weak form of Euclidean division”(弱形式欧几里得除法):高位和低位各自解密出来可能不是完美的数学上的商和余数,因为它们互相包含了一个”互补”的误差项,但它们合起来依然能完美还原原始消息。
第二部分:Decompose 与模数消耗
Q2: Decompose 机制与实现细节
问题:
- 为什么论文中通过 decompose 能够减少模数消耗?
- “First, we need a way to homomorphically decompose a large bit-size plaintext into smaller pieces” 这个是什么意思?
- 1.1中的”Note that relying on smaller precision arithmetic for fixed-point or floating-point arithmetic is a standard technique”,这是什么意思,为什么要提这句话?
- 1.1中,Attempt 1 里明文属于 ,为什么 Attempt 2 中密文却是 ?对于 CKKS 方案,明文和密文多项式系数有什么大小限制吗?
- 1.1节最后的图中在说些什么?
回答:
2.1 为什么通过 Decompose(分解)能够减少模数消耗?
核心逻辑:将“大数的乘法”转化为“小数的乘法”,并舍弃微不足道的部分。
在标准 CKKS 中,模数消耗(Rescaling 消耗的比特数)直接取决于你的缩放因子(Scaling Factor )。
- 如果你要计算两个很高精度的数(比如需要 100-bit 精度),你的 必须很大(比如 )。
- 做一次乘法后,噪声变大,你需要除以 (Rescale)。这意味着你一次就要消耗掉 100-bit 的模数链。模数很快就用光了。
Decompose 的做法: 它把一个大数 拆成两半:高位 和 低位 ,即 。 这里 和 的数值范围都变小了(比如原来是 100-bit,现在两个都是 50-bit)。
- 现在做乘法时,我们实际上是在做 。
- 展开后是:。
- 关键点:方案中的
Mult2算法会扔掉最后那一项 (因为它是“低位乘低位”,对总精度的影响极小)。 - 这样一来,每个分量()只需要较小的缩放因子就能维持精度。
- 结果:每次操作消耗的模数取决于分块的大小(比如 50-bit),而不是整个大数的大小(100-bit)。模数消耗减半,意味着你可以做更多层乘法,或者用更小的参数实现同等精度。
2.2 “Homomorphically decompose a large bit-size plaintext into smaller pieces” 是什么意思?
这句话拆开来看:
- Large bit-size plaintext:一个数值很大的明文(例如 )。
- Smaller pieces:把它拆成两个较小的数,比如按 拆分,拆成商 和余数 。
- Homomorphically(同态地):这是最难的地方。
- 如果你有私钥,解密出 12345,算出 123 和 45,再加密回去,这很简单。
- 但是”同态”意味着你手里只有密文 ,你没有私钥,却要通过计算生成两个新的密文 和 。
为什么这很难? 因为“取余数”和“整除”是非线性运算,在同态加密(尤其是 CKKS 这种近似计算)中非常难以实现。这篇论文的创新点就在于提出了一种高效的(虽然是近似的)方法来在密文状态下完成这个拆分。
2.3 关于 1.1 中提到的”Standard technique for fixed-point…”
意思是:不要觉得”扔掉低位乘低位”这个操作很奇怪,这在经典计算机科学里是很常见的操作。
- Fixed-point arithmetic(定点数算术): 当计算机硬件只支持 32 位乘法,但你需要 64 位精度时,程序员会把 64 位数拆成两个 32 位数来算。
- 在计算 时,如果不把所有交叉项都算出来,而是为了效率舍弃掉最小的那个尾数项,结果依然是足够精确的。
- 为什么要提这句话? 作者是在为他们的算法设计做辩护(Justification)。他们在
Mult2算法中为了省模数,故意扔掉了 这一项。如果有审稿人质疑“这不会导致精度损失吗?”,作者就可以说:“会损失一点点,但这是浮点数/定点数计算领域的标准做法,完全在可接受范围内。”
2.4 Attempt 1 和 Attempt 2 的模数问题,以及系数限制
这里你观察得很细致!
Attempt 1 vs Attempt 2:
- Attempt 1 (Decompose then Encrypt): 这是在说“如果我们在明文阶段就拆好”。比如我有明文 ,我先算出 ,然后分别加密成 。这里 指的是多项式环,意思是系数很大也没关系,反正还没加密。
- Attempt 2 (Encrypt then Decompose): 这是论文真正采用的方法。这里密文模数是 。
- 为什么是 ? 为了方便做除法。
- 作者想在密文上通过乘以 来提取高位。在模 的算术中,“除以 ”其实是乘逆元。但如果模数本身是 的倍数,我们可以通过简单的系数截断或者**重缩放(Rescaling)**操作来模拟“移位”和“除法”的效果。把模数设为 可以让高位部分(Quotient)很自然地落在一个模数为 的密文空间里(即 )。
CKKS 的系数限制:
- 明文多项式: 系数通常受限于缩放因子 或 。在编码后,系数大约是 的大小。
- 密文多项式: 是一对多项式 ,它们的系数是在 范围内的整数(模 )。
2.5 这个截图(1.1节最后)到底在说什么?
这段话是在解释论文提出的**“弱形式同态欧几里得除法”(Weak Homomorphic Euclidean Division)**的原理,以及为什么即便有误差,它也是可用的。
逻辑流:
- 目标: 我们把密文 拆成了 ,希望 是商(高位), 是余数(低位)。理想情况是:。
- 现实问题: CKKS 解密是有噪声(Error)的。所以解密出来的商 不一定等于完美的整数商 。
- 设: ( 是商的误差)。
- 互补效应(核心):
- 由于总的消息 必须守恒(),即:
- 如果你解密出的商多了一个误差 ,那么这一项被乘了 ,变成了 。
- 为了让等式成立,解密出的余数 就必须自动包含一个相反的误差来抵消它。
- 所以余数的解密值变成了:,其中 。
- 结论(Weak form):
- 虽然“余数部分”的误差 很大(它是商误差的 倍),看起来很吓人。
- 但是,因为 拆分后的余数多项式 本身系数很小(这是由分解操作强制保证的),所以解密出来的结果在数学上依然成立。
- 这就叫“弱”形式: 我们得到的不是完美的“商”和“余数”,而是一个“带了一点误差的商”和一个“带了巨大补偿误差的余数”。但妙就妙在,只要把它们重新组合起来,误差会互相抵消,还原出原始的 。
简单总结截图的意思: “我们把密文拆了。虽然拆出来的‘商’和‘余数’各自都有点误差(尤其是余数的误差看起来很大),但因为解密公式是线性的,这些误差在重组时会正好抵消。所以这个拆分是安全的。”
第三部分:误差分析与精度控制
Q3: Decompose 的精度影响与误差抵消机制
问题:
- Decompose后最终结果的精度有影响吗?
- 对于解密密文的高位数据 ,将其解密得到 ,问题是,这个误差 是随机的,而且我只会得到一个解密结果,我并不能推测出高位解密后的误差 是多少,同样,对于解密密文的低位数据也是如此,那么我怎么可能确保高位和低位的解密误差抵消,从而保证结果正确?
回答:
这两个问题直击了该方案最反直觉的核心。别担心,你的困惑非常合理——通常我们在密码学里谈论”误差”时,默认它是随机且不可控的。但在这里,情况完全不同。
3.1 Decompose 后最终结果的精度有影响吗?
答案:有影响,但影响很小,且是可控的。
精度损失主要来自两个方面:
-
舍弃了“低位 低位”项(算法设计层面的损失):
- 在 算法中,为了节省模数,作者故意扔掉了 这一项。
- 想象你在算 。
- 。
- 那个 就是“低位 低位”。扔掉它对结果的影响非常微小(远小于 CKKS 本身自带的噪声)。这在数值计算中是标准的舍入操作。
-
噪声放大的风险(数学层面的损失):
- 虽然我们下面会说误差能抵消,但因为“低位部分” 实际上承载了放大了 倍的误差(即 ),如果不加控制,经过多次乘法后,这个 可能会增长得比正常 CKKS 快一点。
- 解决办法: 论文提出定期进行 Recombine(重组) 操作。把 合并回一个普通密文 ,让那些大的正负误差物理上抵消掉,然后再重新分解。这相当于“重置”了误差状态,保证了长期运行的精度。
结论: 只要参数选得好(比如适时重组),最终精度和标准 CKKS 几乎是一样的。
3.2 既然误差是随机的,我怎么能保证高位和低位的误差刚好抵消?
这是一个极其精彩的问题!你的直觉是:“高位解密出 ,低位解密出 ,这俩 error 都是随机的,凭什么加起来正好是 0?”
真相是:低位的误差 根本不是随机的,它是被”强行制造”出来抵消高位误差的。
请看下面的推导,我会用一个**“切蛋糕”的例子**来打破这个迷思。
1. 数学上的”强制绑定” 并不是先算出高位,再独立算出低位。低位是根据高位算出来的。
论文中的分解过程()本质上执行了以下逻辑:
- 计算商(高位): 。
- 这一步确实引入了随机误差,因为 会导致精度丢失。
- 计算余数(低位): 。
- 注意! 这里是严格的等式。余数被定义为“原数减去(除数乘以商)”。
2. 解密时的”魔法”
现在我们来解密(记解密函数为 ,它是一个线性函数,即 )。
我们把上面的等式两边同时解密:
移项得到:
这说明什么?
- 不管 (高位)错得有多离谱,哪怕它算错了一万八千里。
- (低位)都会自动包含一个“负的一万八千里”。
- 因为 在生成的时候,就是用总量减去高位得到的。剩下的就是低位,无论剩下的是什么。
3. 直观类比:切绳子
假设你有一根绳子,总长度是 100.5 米(这就好比原密文 )。
- 你想把它切成两段,一段是整数部分(高位),一段是小数部分(低位)。
- 你测量了一下,觉得整数部分应该是 50 米,于是你切了 50 米下来(这是 )。
- 那么剩下那段是多少?必然是 50.5 米(这是 )。
- 当你把它们拼回去:。结果正确。
现在,假设你“高位”切错了(产生了随机误差):
- 你手抖了,第一刀切成了 51 米(高位误差 )。
- 那么剩下那段绳子是多少?物理上必然变成了 49.5 米(低位自动变成了 )。
- 当你解密(把两段绳子拼起来)时: 结果依然正确!
总结
你不需要推测误差是多少,也不需要手动去抵消它。
误差抵消是由代数结构保证的。因为 的定义就是 ,所以当你把它们按 加回去时,你只是把减去的东西又加了回来,结果必然还原回原始的 (以及原始的 )。
所以,高位的误差是随机的,但低位的误差是”高位误差的镜像”,它们是互补的。
第四部分:Mult² 算法详解
Q4: Relinearization 和 Rescaling 的改进
问题:帮我详细解释 1.2 Multiplication of decomposed ciphertexts 中的 Relinearization and rescaling 部分,解释为什么要这么做。
回答:
这一部分确实比较绕,但如果抓住了**“高位误差放大”和”强制互补”**这两个核心逻辑,就很容易理解了。
为了实现分解密文的乘法,论文重新定义了 (重线性化)和 (重缩放)。我们来看看为什么要改,以及怎么改的。
4.1 为什么不能直接用标准的 Relin 和 RS?(痛点:误差放大)
假设我们有两个分解好的部分 ,其中 。
如果我们“天真”地对它们分别做标准操作:
- 对高位操作: 。
- 问题来了: CKKS 的 Relin 操作会引入一个小的随机噪声 。
- 所以 。
- 但在最终恢复数据时,高位是要乘以 的!
- 这就导致最终误差变成了 。
- 后果: 本来 很小,但被放大了 倍(比如放大 倍),这个巨大的误差会瞬间摧毁整个计算结果的精度。
结论: 我们绝对不能允许在高位 上直接引入“未被低位补偿”的独立误差。
4.2 Relin²:如何安全地重线性化?
为了解决上述问题,作者设计了 。它的核心思想是:先把高位”还原”到原来的量级,处理完再拆开。
步骤解析:
公式:
这里做了三件事:
-
放大高位():作者没有直接处理 ,而是先把它乘上 。这样它的量级就和原始密文一样了。
-
在大量级上做 Relin:计算 。此时引入的噪声 是加在 上的,也就是加在”总数”上的。这个噪声没有被额外放大。
-
重新分解(DCP):把处理完的结果再次通过 拆成新的商和余数。妙处:这一步拆分会自动把刚才 Relin 引入的噪声分配到新的”低位”里去(就像我们之前讨论的”切绳子”原理)。
总结: 避免了直接在高位加噪声,而是把噪声加在整体上,再通过分解操作把噪声”挤”到低位去。
4.3 RS²:如何安全地重缩放?
(Rescaling)的作用是把密文除以缩放因子 并取整。这也是一个会引入舍入误差的操作。
公式解析:
这简直就是我们上一轮讨论的**“切绳子/互补误差”**逻辑的直接应用!
让我们看看为什么要这么写(假设 ):
-
新高位(New High): 直接对高位做重缩放:。
- 这一步肯定有舍入误差:。
- 就像之前说的,这个 如果不处理,会被放大 倍。
-
新低位(New Low): 作者是怎么算低位的? (注:公式里的 就是重组后的 Total 密文)。
- 这步操作的物理含义:
- 因为 。
- 如果 包含了正向误差(切多了),那么在计算 时,因为减去了 ,这个正向误差就被减掉了。
- 结果: 会自动变成一个包含“负向补偿误差”的值。
总结: 的做法是:先算高位,然后用“总数”减去“高位占的部分”来强行定义低位。 这样就强迫低位吸收了高位 Rescaling 过程中产生的所有舍入误差,保证了 的恒等关系。
全文总结
为什么要这么麻烦地设计 和 ?
一句话解释:为了防止“高位”上的微小操作误差被系数 放大成灾难。
所有这些操作的核心策略都是:
- 不要独立修改高位。
- 要么先还原成整体再修改(Relin²)。
- 要么利用代数恒等式
Total - High = Low,强行让低位去背锅(RS²)。
Q5: Relin² 的输入和数据结构
问题:Relin² 的输入是什么?是上一步 tensor 后的结果?以及 这里的 0 是什么意思?
回答:
这两个问题问到了算法的数据结构和运算逻辑的细节,非常棒。
5.1 Relin² 的输入是什么?
简短回答: 是的,它的输入正是 Tensor²(上一步) 的输出结果。
详细解释:
我们需要回顾一下 CKKS 乘法的标准流程:Tensor Relin Rescale。
-
Tensor² 的输出(即 Relin² 的输入): 在标准 CKKS 中,两个密文相乘(Tensor)后,密文会膨胀。原本密文是 2 个多项式 ,相乘后变成了 3 个多项式 。这被称为“度为 2 的密文”(Degree-2 ciphertext),因为它包含密钥 的二次项 。
在 方案中,因为我们维护的是一对密文 ,所以
Tensor²的输出是一对“膨胀”了的密文:- :是一个包含 3 个多项式的密文(高位部分)。
- :也是一个包含 3 个多项式的密文(低位部分)。
Relin² 的任务就是把这两个“膨胀”的 3 元素密文,压缩回正常的 2 元素密文 。
5.2 (0, Relin(č̌t)) 这里的 0 是什么意思?
简短回答:这里的 0 代表一个**“全零密文”(Zero Ciphertext),它是为了保持”密文对”格式**而存在的占位符。
详细逻辑:
公式如下:
请注意,整个系统的基本数据单元是 “密文对” (Pair),即所有运算结果都必须长这样:(高位部分, 低位部分)。
我们来看看加号两边分别是什么:
-
部分 A(处理高位): 这个函数会将输入分解,输出一个对:。 这是把高位的 Relin 结果拆解后得到的商和余数。
-
部分 B(处理低位): 我们在做 ,这是对低位进行的压缩操作。 这个操作的结果理应只属于**“新的低位”,而不应该影响“新的高位”。 但是,为了能和“部分 A”进行向量加法,它必须也被写成一个对**的形式。
所以作者构造了这样一个对:
- 高位位置: 放一个
0(全零密文)。意思是我这一步操作对高位没有贡献。 - 低位位置: 放 。
- 高位位置: 放一个
最终的加法过程(向量加法):
总结:
那个 0 就像我们在做向量运算 时的那个 0 一样,只是为了让维度对齐,确保 只被加到结果的低位分量上,而不污染高位分量。
Q6: Growth of the low part(低位膨胀问题)
问题:详细介绍 1.2 中的 Growth of the low part。
回答:
这一部分描述了 算法面临的一个核心挑战,以及作者提出的解决方案。我们可以把它称为**“低位部分的膨胀问题”**。
6.1 现象:低位部分(Low Part)为什么会变大?
起初,当我们刚对一个密文进行分解(Decompose)时: 根据带余除法的定义,低位 是余数,所以它的系数绝对值很小,被严格限制在 。
但是,当我们开始对分解后的密文进行乘法运算(特别是 步骤)时,低位部分会迅速变大。
原因分析: 回顾一下乘法的交叉项逻辑。假设我们有两个数 和 :
试图计算 。根据 的定义,新的低位部分(在逻辑上)大致对应于交叉项: (注:这里为了直观忽略了具体的缩放因子和 的系数调整,只看量级)
- 和 是“商”,代表了数值的主要部分,数值很大。
- 和 是“余数”,起初很小。
- 相乘结果: 一个“大数”乘以一个“小数”,结果会比原来的“小数”大得多。
结论: 经过一次乘法后,新的低位部分不再是简单的“余数”了,它混合了高位的信息,导致其数值量级显著增长。如果连续做多次乘法,这个膨胀会呈指数级累积。
6.2 危害:变大有什么问题?
如果低位部分 长得太大,会引发两个严重后果:
-
精度雪崩(主要原因):还记得 为了省模数,在 Tensor 步骤中直接丢弃了 这一项吗?
- 起初:因为 很小,所以”小 小”微不足道,丢了也就丢了,误差很小。
- 膨胀后:如果 变得很大,那么 就变成了一个巨大的误差项。这时候再把它扔掉,就会导致计算结果严重偏离正确值。
-
可能溢出:如果 的系数增长到超过了模数(虽然我们在 中讨论,但实际实现还是有物理限制的),或者超过了为了保证”弱欧几里得除法”成立的界限,整个数学假设就会崩塌。
6.3 解决方案:重组与再分解 (Recombine and Decompose)
为了解决这个问题,作者提出了一种类似“定期重置”的策略。
策略名称: Recombine and Decompose (RCB DCP)
操作步骤: 当发现低位膨胀到一定程度(或者在进行了固定次数的乘法后),执行以下操作:
-
Recombine (RCB): 把高位和低位拼回去,变成一个普通的单密文。 在这个加法过程中,低位中积累的那些“大数值”会被加到高位上去(进位),或者与高位的数值合并。
-
Decompose (DCP): 立即对这个 再次执行分解操作。
效果:
- 新的低位 是通过强制取余得到的。
- 强制归零: 无论之前膨胀得由多大,经过这一步,新的低位系数又被强行压回了 的范围内。
- 误差重置: 之前累积的可能导致丢弃误差变大的因素被消除了。
4. 实验结论(来自 Figure 1)
论文在 1.2 节末尾和实验部分提到了一个具体的数据(参考 Figure 1):
- 对于特定的参数(),低位膨胀是显而易见的。
- 如果不处理,误差会指数级上升。
- 最佳实践: 作者发现,在连续执行 6 次 乘法后,执行一次“重组与再分解”是性价比最高的。既避免了频繁操作带来的计算开销,又控制住了误差的增长。
总结
- 问题:乘法会让”低位”不再是单纯的”余数”,而是包含了高位的交叉项,导致数值越来越大。
- 后果:低位变大 丢弃项变大 精度丢失。
- 解决:也就是”洗牌”——定期把牌收回来(Recombine)重新发一次(Decompose),强行把低位压回初始的小状态。
第五部分:参数优化与模数分配
Q7: 不对称分解的效率分析
问题:之前有提到,将密文维度从 100bits,分解为高位低位各 50bits,可以节省一半模数,那如果分解的大小不一致呢?比如高位 60bits,低位 40bits 这种情况下是怎样的?
回答:
这是一个非常敏锐的问题!这涉及到优化理论中的**“均值不等式”**原理在密码学参数选择中的应用。
简短的回答是:不对称分解(如 60/40)会导致效率降低。50/50 分解是数学上的最优解(即模数消耗最小)。
为了解释为什么,我们需要回到该方案中控制精度和模数消耗的核心公式。
7.1 核心公式回顾
在 方案中,我们要维持的总精度(Scaling Factor )大约等于“分解因子”乘以“消耗掉的模数”:
- ():决定了**低位部分(Low Part)**的大小。
- 如果你选 ,低位就是 40 bits。
- 如果你选 ,低位就是 60 bits。
- :是我们在做 Rescaling 时扔掉的模数(也就是我们要消耗的成本)。
制约条件(瓶颈): 论文在误差分析(Theorem 4.8 和 4.9)中指出,为了保证计算结果正确,扔掉的模数 必须足够大,至少要比低位部分的平方稍大一点,否则低位的误差项 会爆炸。 简单来说,必须满足: (注:严格来说误差项是 Low Low / ,如果要让这一项变小, 的比特数最好不小于 Low 的比特数)
7.2 场景分析:目标总精度 100 bits
我们现在的目标是 。这意味着 。
我们来看看不同切分方式的代价:
1. 对称分解(50 / 50)—— 最优解
- 低位大小 (): 50 bits。
- 模数消耗 (): 为了凑齐 100 bits,且满足 ,我们选 bits。
- 检查误差: ,误差被压制住了,没问题。
- 最终代价: 消耗 50 bits 模数。
2. 不对称:低位小,高位大(40 / 60)
即 (低位 40 bits),剩下的高位承载 60 bits 的数值。
- 低位大小 (): 40 bits。
- 模数消耗 (): 必须满足两个条件:
- 总和 100:。
- 压制误差:。
- 检查误差: 满足条件。
- 最终代价: 消耗 60 bits 模数。
- 亏了! 本来只需要消耗 50 的,现在消耗了 60。因为虽然你的低位变小了,但为了维持总精度,你不得不把那个 设得很大来补足剩下的精度。
3. 不对称:低位大,高位小(60 / 40)
即 (低位 60 bits),剩下的高位承载 40 bits 的数值。
- 低位大小 (): 60 bits。
- 模数消耗 (): 必须满足两个条件:
- 总和 100:。
- 压制误差(关键): 论文要求 至少要能包住低位。但这里 !
- 如果只用 40 bits 的模数去压制 60 bits 的低位噪声,误差项 。这会直接摧毁精度。
- 强制修正: 为了不让误差爆炸,你被迫必须让 至少也有 60 bits(甚至更大)。
- 最终结果:
- 如果强行选 ,精度全毁,方案不可用。
- 如果为了可用选 ,那么总精度变成 bits(超出了需求),且消耗了 60 bits 模数。
- 又亏了!
总结
这就好比你要围一个 面积为 100 的矩形(面积代表总精度 ),而模数消耗是矩形的较长边(因为 必须既补足精度,又要盖过 ,取两者的最大值)。
- 正方形(50 50): 边长为 50。这是让边长(模数消耗)最小的方案。
- 长方形(40 60): 边长变成了 60。模数消耗变大了。
所以,均分(Symmetric Decomposition) 是让模数消耗降到最低()的唯一数学极值点。任何偏离均分的操作,都会导致你需要消耗更多的模数来达到同样的精度,或者在同等模数下得到更差的精度。
Q8: 模数消耗的平方关系疑问
问题:你不是说”扔掉的模数 必须足够大,至少要比低位部分的平方稍大一点”,为什么示例比较的时候却没有平方?
回答:
这是一个非常非常棒的质疑!你发现了我在上一条回答中为了简化直觉而表述不够严谨的地方。
让我根据论文的数学推导,为你精确地纠正这个概念。
结论先行:
你是对的,直觉上”低位平方”应该是 。但是,在 的算法结构中,有一个关键步骤(Tensor 后的隐式除法)抵消掉了一个 。所以,最终的数学约束变成了**“线性关系”**,而不是”平方关系”。即:模数 的比特数 低位部分 的比特数。
8.1 为什么”平方”变成了”线性”?(数学推导)
让我们打开论文 第 8 页 “Modulus consumption” 这一小节,作者在这里给出了精确的推导。
步骤 A:噪声源头确实是“平方”
在做 时,我们扔掉的项是 。
- 设低位大小为 。
- 那么扔掉的这一项的大小确实是 。
步骤 B:算法自带的“除法效应”
请注意 的逻辑是模拟 的效果(因为我们提取的是商)。 根据 Lemma 4.2, 的结果实际上被除以了 (即 )。
- 这一步把噪声从 缩小到了:
步骤 C:Rescaling 的除法
最后,我们执行 (重缩放),这会把结果再除以模数 。
- 最终残留的噪声大小是:
步骤 D:约束条件
为了让这个最终误差很小(比如小于 1,或者小于某个常数),分母必须大于分子: 两边取对数(Bit-size):
这就是为什么我在比较时是直接比较比特数(50 vs 50),而不是比较平方。
2. 重新审视 60/40 的例子
现在用这个精确的数学关系,我们再看一遍为什么“均分”最优。
假设目标总缩放因子 ,我们需要 。
方案 1:均分(50 / 50)
- 低位 。
- 根据约束 ,我们需要 。
- 为了凑齐 100 总量,我们正好取 。
- 结果: 完美匹配,模数消耗 50 bits。
方案 2:低位大(60 / 40)—— 你的疑问点
- 低位 (这意味着噪声源头 是 120 bits,被抵消一次后剩 60 bits)。
- 剩下的空间留给模数: bits。即 。
- 检查约束: 误差是 (约 100 万)! 这对于小数运算来说是巨大的精度灾难。
- 结论: 这个配置虽然凑够了 100 bits 总量,但因为模数压不住噪声,方案不可用。
方案 3:低位小(40 / 60)
- 低位 。
- 为了凑 100 总量,模数 。
- 检查约束: 。满足!而且 ,精度非常高。
- 代价: 虽然精度很高,但你消耗了 60 bits 的模数。
- 结论: 方案可用,但比 50 bits 方案更贵(模数消耗更大)。
总结
我在之前的回答中说“至少要比低位部分的平方稍大一点”,这是口语表达上的失误,容易产生歧义。更准确的说法是:
“模数 必须足够大,以抵消掉‘低位平方项’在经过算法内部除法后残留的影响。”
而这个“残留的影响”,在比特数上,正好就等于低位的比特数。
所以:
- 低位 50 bits 模数至少要 50 bits。
- 这就是 50/50 分割成为最优解的数学原因(Sum 为定值,求 Max(Item) 的最小值)。
Q9: Tensor² 中的除法效应
问题:你提到的”请注意 Mult² 的逻辑是模拟 的效果(因为我们提取的是商)。根据 Lemma 4.2,Tensor² 的结果实际上被除以了 (即 )。“这不会对结果产生什么影响吗?
回答:
这是一个非常敏锐的直觉!通常我们在数学上把结果除以 ,数值不就变了吗?
但在这里,答案是:这不仅不会对结果产生负面影响,反而是为了维持计算正确性所”必须”的步骤。
原因在于 CKKS 的缩放因子(Scaling Factor)机制。
我用最通俗的逻辑给你拆解一下:
9.1 CKKS 的标准流程:必须”除掉”一部分
在 CKKS 中,我们不是直接计算 ,而是计算放大后的整数。 假设缩放因子 (比如 )。
- 数 A 变成了 。
- 数 B 变成了 。
做乘法时发生了什么?
注意到了吗?结果的缩放因子变成了 (即 )。 如果不处理,下次再乘就会变成 ,数值瞬间溢出。 所以,CKKS 算法强制要求:做完乘法后,必须把结果除以 ,让它变回 的规模。
- 标准 CKKS 的做法: 也就是 Rescaling 步骤,直接除以一个模数 。
2. 的流程:分两步“除”
在 方案中,作者把这个“必须除掉的 ”拆成了两部分来实现。 设定: (例如:,拆成 和 )。
第一步:(隐式除法) 正如你引用的 Lemma 4.2,这一步让结果被除以了 。 此时结果的缩放规模从 变成了:
第二步:(显式除法) 这是算法最后的重缩放步骤,会再除以模数 。 此时结果的缩放规模变成了:
最终效果: 因为我们预先设计好了 ,所以:
3. 为什么 Lemma 4.2 会造成除法效果?
为了让你更放心,我们简单看一下 Lemma 4.2 为什么会产生“除以 ”的效果。
逻辑如下:
- 我们的分解是 (忽略低位)。
- 做乘法时,我们计算的是 。
- 这里 其实是 。
- 这里 其实是 。
- 所以乘出来的结果 。
- 但是! 的输出格式是“商和余数”。根据重建公式 ,这个结果会被乘回一个 。
- 综合算一下:
总结
你担心的“结果被除了 ”是真实发生的,但这不是误差,而是功能。
- 标准 CKKS:一次性除以 。
- :先由 隐式除以 ,再由 显式除以 。
这两者殊途同归,最终都把乘法产生的 缩放回了 ,保证了后续计算可以继续进行。
Q10: RS² 中模数消耗减少的本质
问题:原来如此,是因为 RS² 中需要显示除法步骤中除以的模数变小了,因此才导致模数消耗更少?
回答:
完全正确!你已经抓住了这篇论文最本质的”省钱之道”。
简单来说:我们把原本需要”付费”完成的除法,拆成了一半”付费”和一半”免费”来做。
我来给你算一笔账,你立刻就明白了:
10.1 任务目标:把数字缩小 倍
假设为了维持精度,我们需要总的缩放因子 。 也就是说,做完乘法后,我们需要把数据缩小 倍。
2. 标准 CKKS 的做法(全额付费)
在标准 CKKS 中,缩小数据唯一的方法就是 Rescaling(重缩放)。
- 操作: 物理上把密文除以一个模数 。
- 代价: 这个 必须等于 。
- 后果: 你的模数链(Modulus Chain)一下子就被“吃掉”了 100 bits。
- 消费单: 100 bits 模数。
3. 的做法(AA制,但有一半人逃单了)
作者把 拆成了两部分: 和 。
-
步骤 1:(“免费”的除法)
- 如我们刚才讨论的 Lemma 4.2,通过代数结构的重组,这一步在数学上让数据缩小了 倍。
- 关键点: 这一步是靠“把高位系数移位”实现的,并没有消耗掉密文模数链上的任何一个质数。
- 消费单: 0 bits 模数(这是纯粹的数学变换)。
-
步骤 2:(“付费”的除法)
- 这一步是真正的 Rescaling,需要物理除以模数 。
- 因为只需要再缩小 倍就够了,所以我们只需要消耗一个 bits 的模数 。
- 消费单: 50 bits 模数。
4. 最终对比
| 方案 | 总缩放效果 | 实际消耗的模数 | 结论 |
|---|---|---|---|
| 标准 CKKS | 100 bits | 贵,能做的层数少 | |
| Mult | 50 bits | 省了一半! 能做更多层 |
总结:
正是因为 这一步只需要处理剩余的那一半缩放(),所以它消耗的模数比标准做法小得多。而另一半缩放()被算法的结构设计给”白嫖”了。这就是这篇论文降低模数消耗的秘密武器。
Q11: 为什么不能白嫖 100%?
问题:那为啥不直接白嫖 100%?
回答:
这是一个非常符合经济学原理的提问:既然有免费午餐,为什么不全吃免费的?
答案非常残酷:因为”免费”的那部分(),副作用太大,必须用”付费”的那部分()来治病。
如果想白嫖 100%,你会直接死在噪声爆炸上。
我来给你演示一下,如果你尝试”白嫖 100%“会发生什么灾难。
11.1 贪心实验:试图白嫖 100%
假设目标总缩放因子 。 你想让“免费的” ,让“付费的” (即不消耗模数)。
后果推演:
-
分解阶段(Decompose): 你把密文分解为 。
- 因为 ,根据定义,你的低位部分(余数) 的大小可以达到 。
- 注意: 这个“低位”现在是个庞然大物,它本身就包含了巨大的数值。
-
乘法阶段(Tensor): 我们在做乘法时,扔掉了一项 (低位 低位)。
- 因为 大小是 ,所以这一项的大小约为 。
- 虽然 Lemma 4.2 的机制帮我们除了一次 (),但剩下的噪声依然高达:
- 现状: 你的计算结果里混入了一个大小为 的随机噪声。
-
重缩放阶段(Rescale): 这是原本用来消除噪声的步骤。 公式是:除以 。 但因为你太贪心,设了 (为了不消耗模数)。
- 结果: 。
- 最终误差: 。
结局: 你的真实数据可能只有几十 bit,但误差高达 100 bit。有效信号完全被噪声淹没了,解密出来全是乱码。
2. 原理解析:为什么必须 50/50?
这里的核心制衡关系是: 制造噪声,而 消除噪声。
- 制造噪声: 越大,分解出来的“余数”(低位)就越大,乘法产生的“垃圾项”就越大。垃圾项的大小与 成正比。
- 消除噪声: 只能负责“隐式”消除一部分,剩下的必须靠物理除法 来压下去。
数学上的硬性约束(来自 Theorem 4.8): 为了让最终误差 (或者可控),必须满足: 也就是说: (翻译:你花的钱,必须盖得住你制造的麻烦。)
寻找最优解:
- 我们要求 (定值,比如 )。
- 又有约束 。
- 为了让 (花费)最小,我们只能取边界值:。
这就是为什么 vs 是极限。
总结:
- (免费) 是**“藏污纳垢”**的地方:它越大,藏的噪声(低位)就越大。
- (付费) 是**“清洁工”**:它负责把藏不住的噪声清理掉。
- 如果你让污垢()无限大,却不雇佣清洁工(),房子就炸了。
- 50% 的模数节省,已经是数学上允许的”白嫖”极限了。
第六部分:实验结果与相关工作
Q12: 1.5节和1.6节详解
问题:详细解释说明一下 1.5 节和 1.6 节。
回答:
这两个章节分别负责展示成果(1.5 节)和对比同行(1.6 节)。
简单来说:
- 1.5 节是用数据告诉你:这个方法不仅能算得更深(支持更多层乘法),还能在处理高精度任务时大幅降低硬件压力。
- 1.6 节是学术防御:说明这个方法和以前那些”看起来有点像”的方法有什么本质区别,为什么我们更好。
我为你详细拆解如下:
12.1 第 1.5 节:Concrete examples(具体实例与实验结果)
这一节通过两个具体的应用场景,展示了 (即 Double-CKKS)的威力。
场景 A:增加同态容量(Increased homomorphic capacity)
- 目标: 在硬件参数不变(环维数 ,安全性 128-bit)的情况下,看谁能跑更深的电路(做更多次连续乘法)。
- 对比:
- 标准 CKKS: 只能跑 13 层乘法。
- Double-CKKS: 可以跑 18 层乘法。
- 原理: 因为 Double-CKKS 每一层消耗的模数几乎减半(50 bits vs 100 bits),所以原本的“存款”(总模数预算)可以支撑更多次的“消费”。
场景 B:提高精度与效率(Increased precision)—— 这是最亮眼的部分
- 目标:我们想做 100-bit 高精度的计算(Scaling Factor ),且乘法深度为 8。
- 标准 CKKS 的困境:
- 每次乘法要消耗 100 bits 模数。8 层就要消耗 bits。
- 连锁反应:模数 这么大(>1000 bits),为了保证安全性,环维数 必须很大,只能选 。
- 后果:计算慢,密文极其巨大。
- Double-CKKS 的破局:
- 我们把 100 bits 拆成 。每次只消耗 50 bits 模数。
- 总模数需求大幅降低(只需 bits)。
- 连锁反应:因为模数小了,安全性更容易满足,我们就可以用更小的环维数 (减半了!)。
- 降维打击的数据对比(Table 3):
- 计算速度(Latency):从 270ms 降到 179ms(快了约 1.5 倍)。
- 密文大小(Ciphertext Size):从 14.8MB 降到 5.08MB(只有原来的 1/3)。
- 密钥大小(Switching Key):从 74MB 降到 30.6MB(大幅节省内存)。
总结 1.5:这个技术不仅仅是”省模数”,它通过省模数允许我们使用更小的 ,从而实现了速度、存储、通信的全方位优化。
12.2 第 1.6 节:Related works(相关工作对比)
这里作者主要对比了两个容易混淆或相关的技术路线。
1. Gadget Decomposition(小工具分解)
这是以前在 GSW 方案或 CKKS 的 Key Switching 中常用的技术。
- 原理: 把一个大数拆成几个小数(比如按位拆),为了减少 Key Switching 过程中的噪声增长。
- 缺点: 它会显著增加密钥的大小(Key Size),通常会增加 倍(比如几倍到几十倍)。而且它会拖慢 Key Switching 的速度。
- 本文的区别: 本文的分解是针对乘法(Multiplication)的,而不是 Key Switching。而且,如 1.5 节所示,本文的方法实际上减小了密钥大小(因为 变小了),而不是增加。
2. Module-CKKS / Module-LWE(基于模的 CKKS)
这是一个强有力的竞争对手。Module-CKKS 也是通过把密文变成向量(比如 3 个元素 )来尝试降低维度。
- 对比 Rank-2 Module-CKKS vs. Double-CKKS:
- 结构: Module-CKKS 用 3 个元素,Double-CKKS 用 4 个元素(一对密文,每对 2 个)。看起来 Module-CKKS 更紧凑?
- 模数: 但是! Module-CKKS 依然消耗全额模数(比如 100 bits)。而 Double-CKKS 消耗半额模数(50 bits)。
- 总比特量: 综合算下来(元素个数 模数大小),Double-CKKS 的总比特量比 Rank-2 Module-CKKS 小 33%。
- 计算量: Double-CKKS 只需要 2 次 Relin,而 Module-CKKS 需要 3 次。
- 结论: 当需要高精度()时,Double-CKKS 在空间和时间上都优于 Module-CKKS。
总结 1.6:
作者在说:“别误会,我们不是以前那种会让密钥变大的 Gadget 分解,也不是那种虽然维数小但模数依然很大的 Module-CKKS。我们是真·减半模数,综合性能最优。“
第七部分:CKKS 底层原理深入
Q13: 2.1节中的多个技术细节
问题:
- “The modulus Q is typically a product of RNS integers and, for the sake of efficiency, arithmetic modulo Q is performed in the RNS form whenever possible.” 似乎揭示了有些步骤是不能使用 RNS 表示的?
- 为什么规范嵌入中要选 ?是为了方便进行旋转操作?如果是这样的话,其背后的数学原理是什么?为什么非得是 5?
- 脚注中:“To minimize the numerical errors, it is useful to consider a different scaling factor for each multiplication level of the circuit to be homomorphically evaluated; for the sake of simplicity, we do not consider this optimization” 这是什么意思?实际代码实现中有考虑吗?
- 解密中,在不同的层级解密结果的精度是不一样的?层级越深,精度越低?
- 关于:“We assume that h is set so that the condition holds every time we use RS in this work.” 在 rescale 中,汉明权重 h 不是显然小于 吗?为啥要强调一下?
- 这段话是啥意思?freshly generated ciphertexts、BDec bound 是啥,干啥用的?
回答:
这几个问题依然非常硬核,涉及到同态加密底层数学原理和论文的严谨性表述。我逐条为你解析:
13.1 关于 “arithmetic modulo Q is performed in the RNS form whenever possible”
是的,这意味着某些步骤不能(或很难)直接在 RNS 下进行。
- RNS 的强项: 加法、乘法。因为 和 在 RNS 系统中就是对每个小质数 分别做加法和乘法,完全并行,效率极高。
- RNS 的弱项: 除法、取整、模数切换(Modulus Switching)、比较大小、位分解。
- 在 RNS 表示下(比如 表示为 ),你很难直接知道 到底有多大,也很难直接计算 或者 。
- CKKS 的痛点:
- Rescaling(重缩放): 本质是 。这是除法和取整。
- 本论文的 Decompose: 需要计算 。这涉及到“除以 ”和“取余”。
- 怎么办? 在这些步骤中,通常需要使用复杂的 RNS 扩展算法(如 Bajard-Eynard-Hasan-Zucca 算法或 HPS 算法),在不完全恢复大整数的情况下近似计算除法;或者在极少数情况下,不得不通过 CRT(中国剩余定理)暂时把数据恢复成大整数(或多项式形式),处理完后再转回 RNS。
- 论文语境: 这句话是在给自己留余地。虽然大部分时间都在 RNS 里跑,但到了 Rescaling 或 Decompose 这种非线性操作时,必须使用特殊的算法来处理,不能简单地 component-wise 进行。
2. 为什么规范嵌入(Canonical Embedding)中要选 ?为什么是 5?
是为了旋转(Rotation/Galois Automorphism),背后的数学原理是分圆域的伽罗瓦群结构。
- 背景: 我们工作的环是 ,其中 是 2 的幂(比如 )。
- 伽罗瓦群: 这个多项式对应的分圆域的伽罗瓦群同构于模 的乘法群 。
- 生成元: 对于 为 2 的幂的情况,这个群的结构是 。它有两个生成元:
- -1:对应复共轭(Complex Conjugation)。
- 5:对应槽(Slot)的循环置换。
- 为什么是 5?
- 数学上,对于 , 在模 下的阶(Order)是 。
- 这意味着 可以遍历大部分的指数,从而实现对密文槽(Slots)的遍历和置换。
- 如果我们选 3,它在模 下的行为可能无法生成原本的子群,或者阶数不对。
- 结论: 选 5 是因为在 为 2 的幂次时,5 是乘法群中指数为 1 的那个子群的标准生成元。它能保证把加密在向量里的数据“转”到任何你想要的位置。
3. 关于“不同层级使用不同 scaling factor”的脚注
意思是:为了抵消模数不精确匹配带来的误差,工程上需要微调。
- 理想情况: 假设缩放因子 。我们希望模数链也是 每个都是 。这样 (缩放因子完美保持)。
- 现实情况: RNS 模数 必须是质数。你找不到一个质数正好等于 。你可能找到 。
- 后果: 每次 Rescaling,原本的缩放因子 会变成 。
- 如果 ,那么 就不等于 。
- 算得层数越多, 就会飘得越远。
- 优化(Optimization):
- 现在的库(如 HEaaN, SEAL)不会强制要求 固定。它们会动态记录当前的 是多少。
- 或者,在编码(Encoding)的时候,故意根据这一层对应的模数 来微调输入的 ,使得 正好等于下一层想要的 。
- 论文意思: “我们写论文推导公式时,假定 (完美相等),这样公式好看。但你们写代码时别忘了处理这个问题。” 实际代码中当然考虑了,否则精度会丢得一塌糊涂。
4. 解密结果的精度随层级变化吗?
是的,通常层级越深(剩余模数越小),相对精度越低(或保持不变但更危险)。
但这里要区分两个概念:
- 绝对噪声(Noise Norm): 随着乘法运算,噪声的绝对值在不断变大。
- 相对精度(有效比特位): Rescaling 的目的就是把“信号”和“噪声”同时缩小,试图维持相对精度。
- 但是,Rescaling 本身引入了舍入误差。
- 在 中,Low Part 的误差积累(如 Figure 1 所示)是随层数增加的。
- 结论: 在这篇论文的方案里,如果不进行 Recombine,层级越深,累积的误差越大,解密出来的有效精度(Precision)确实越低。
5. 关于 的假设
这是一个“活着”的底线条件。
- :当前的密文模数。
- :你要除掉的 Rescaling 因子。
- : 这大约等于做完 Rescale 后剩下的模数(即 )。
- :私钥的汉明权重(非零元素个数),它决定了解密时 这一步产生的内在噪声大小。
- 为什么要强调?
- 如果 (剩下的模数)太小,小到比解密本身的噪声(和 相关)还要小,那么解密就会失败,模数这就“彻底干了”。
- 虽然通常 很大,但在最后一层或者极其激进的参数设置下,有可能 Rescaling 后剩下的空间不够了。作者这是在声明数学上的边界条件:“只要你还想继续算,剩下的模数就不能小于私钥噪声的底线。”
6. 关于最后一整段话的含义
这段话非常重要,是在定义**“什么是解密”以及“正确性的标准”**。
A. Freshly generated ciphertexts & BDec bound
- Freshly generated: 刚加密完、还没做过加减乘除的密文。此时噪声最小。
- (Decryption Bound): 这是能正确解密的最大噪声界限。如果密文里的噪声超过这个值,解密出来的消息就会出错(破损)。
- 这句话的意思: 我们选参数时,要保证刚加密出来的密文噪声很小,离“坏掉”()还很远,留出足够的空间给后面的同态运算折腾。
B. “Alternatively… definition as inner product… modulo ”
这是什么意思?
- 标准定义: 在第 层,解密是 。即在当前模数 下取模。
- 替代定义: 不管你在哪一层,我都把你当作整数(或 中的元素),和 相乘,然后直接对最底层的模数 取模。
- 即 。
直接用底层模数模其他层级的密文,对吗?
- 在理论上是对的! 只要密文的有效消息部分 + 噪声部分的总大小没有超过 。
- CKKS 的消息通常很小(缩放后也就几十 bit),噪声也就几十 bit。只要 (比如 60 bit)足够包住它们,那么无论外面的模数 是 1000 bit 还是 2000 bit,对于里面的数值来说,模 和模 的结果是一样的(因为数值本身还没碰触到 的天花板)。
- 用途: 这样做是为了证明方便。如果不这样定义,每次证明都要写“在 下…在 下…”,非常麻烦。统一用 作为参考系,可以简化数学证明的符号系统。
C. “The first formulation is syntactically more convenient…”
- First formulation: 指的是 (标准定义)。
- 为什么更方便? 因为这篇论文主要讲的是 Decomposition 和 Rescaling。
- 论文的核心操作是把密文拆分、重组、切换模数。
- 使用标准定义(当前模数 )能更直观地展示每一步操作后模数是如何变化的(从 变到 )。
- 如果用替代定义(永远 ),虽然证明逻辑自洽,但很难直观体现出”模数消耗”这个论文的核心卖点(因为 是不变的)。所以作者为了展示贡献(reduced modulus consumption),选择了第一种写法。
Q14: 计算与规范嵌入
问题:
- 是怎么计算的?
- 规范嵌入(Canonical Embedding)中要选 为什么是 5?关于这个问题,有什么博客文章的推导过程或论述吗?
回答:
这两个问题直指同态加密(尤其是基于 Ring-LWE/RLWE 的方案如 CKKS、BFV、BGV)的底层核心。一个是关于正确性界限,一个是关于代数结构。
14.1 是怎么计算的?
(Decryption Bound) 指的是为了保证解密正确,密文中所允许的最大噪声界限。
在 CKKS 中,解密公式通常是: 即先计算内积,然后模 。
计算逻辑
为了能正确还原消息(或者近似消息),内积的结果 在模 之前,绝对值不能超过 。否则发生模数回绕(Wrap-around),正数可能变成负数,或者数值产生巨大偏差。
数学上: 我们希望 。所以必须满足:
因此, 的计算公式通常很简单,就是当前模数的一半(减去消息本身的大小):
在实际论文和参数设定中的意义:
- :当前的密文模数。
- :消息的大小(在 CKKS 中由缩放因子 决定,通常 )。
- :噪声。
- 判断标准: 只要你的噪声 (包含各种乘法、重缩放积累的误差)小于 ,解密就是安全的。一旦噪声超过 ,解密就失败了。
2. 规范嵌入中为什么要选 ?为什么是 5?
这是一个纯粹的数论问题,源于分圆域(Cyclotomic Fields)的伽罗瓦群结构。
结论
选择 5 是为了构造模 乘法群的一个生成元,从而能够遍历所有的槽(Slots)。
数学推导过程
-
背景:
- 我们使用的环是 ,其中 是 2 的幂()。
- 这对应于 -分圆域 ,其中 。
- CKKS 的 SIMD 操作(Batching)依赖于在这个域上的自同构(Automorphism)。
-
伽罗瓦群结构:
- 这个域的伽罗瓦群 同构于模 的单位群(乘法群):
- 我们需要知道这个群 长什么样。
-
核心定理(单位群结构): 对于 (且 ),模 的乘法群不是循环群(没有单一生成元),而是同构于两个循环群的直积:
- (阶为 2 的子群): 由 -1 生成(对应于复共轭操作 )。
- (阶为 的子群): 需要一个元素,它在模 下的阶是 。5 就是满足这个条件的最小整数。
-
为什么是 5?验证一下:
- 我们需要一个数 ,使得 的幂次能生成形如 的所有数。
- 尝试 3: 。3 的性质稍显复杂。
- 尝试 5:
- …
- 数学归纳法可以证明:,且 。
- 这意味着 5 的阶确实是最大可能的 (即 )。
-
实际意义(Slot 映射):
- 我们的明文槽向量(Slots)是通过 来索引的。
- 如果我们只用 5 进行旋转(Rotation),我们可以访问到一半的槽(因为 5 生成了 个元素)。
- 另外一半槽通过复共轭(-1)来访问。
- 公式: 任意一个位置索引 都可以唯一表示为 。
- 这就是为什么所有的同态旋转操作(Rotate)底层都是在算 。
推荐的阅读资料与博客
关于这个问题,通常在介绍 HElib、SEAL 或 Ring-LWE 基础的硬核文档中会有详细推导。
-
推荐论文(圣经级):
- Smart and Vercauteren, “Fully Homomorphic Encryption with Relatively Small Key and Ciphertext Sizes” (2010): 这篇论文详细讨论了 SIMD 操作和超立方体结构,确立了 作为生成元的标准。
- Gentry, Halevi, Smart, “Homomorphic Evaluation of the AES Circuit” (2012): 这里面有关于 Batching 和 Galois Automorphism 的详细工程实现讨论。
-
推荐博客/讲义:
- Vadim Lyubashevsky 的讲义 “A Toolkit for Ring-LWE Cryptography”: 这是一个非常好的综述,里面有关于环结构和自同构的数学解释。
- Microsoft SEAL Manual: 虽然是说明书,但它的原理部分对 的解释非常清晰,明确提到了 的映射关系。
- 搜索关键词: 建议用 Google 搜索以下关键词组合:
Structure of multiplicative group modulo 2^kGalois group of cyclotomic field 2^nCKKS batching slot 5 generator
- StackExchange: Math StackExchange 上有一个经典问题:“Why is the multiplicative group modulo not cyclic?” 里面会详细证明为什么生成元是 5 和 -1。
简而言之:选 5 是因为它是模 乘法群中那个大循环子群的标准生成元,能保证你“转”遍除了复共轭以外的所有位置。
BOB:1. 为什么系数选定在[-0.5 Q ,0.5Q],而不是[0,Q]? 2. Gadget decomposition was for example introduced to avoid modulus consumption in key switching. It comes in several flavours, including bit decomposition [5, 6], digit decomposition [13] and Residue Number System (RNS) based decomposition [3, 20, 21]. 为什么Gadget decomposition能够减少模数消耗??以及这几种Gadget decomposition具体是怎么做的?
这两个问题问得非常到位。第一个涉及到同态加密的数理基础(Norm),第二个涉及到同态加密中**密钥切换(Key Switching)**的核心技术。
1. 为什么系数选定在 ,而不是 ?
这不仅仅是一个表示习惯的问题,而是由 RLWE(Ring-LWE)问题的噪声(Error)机制决定的。
核心原因:为了正确衡量“噪声”的大小(最小绝对值)。
在同态加密中,安全性依赖于噪声 是一个“很小”的值。解密成功的条件通常是:噪声的范数(Norm)小于模数的一半。
举个直观的例子
假设模数 。 我们有一个噪声 。
-
在 的表示法中: 。 如果你直接看数值, 是一个很大的数,接近 。在计算噪声大小时,如果你认为噪声是 ,你会觉得解密肯定要失败了(因为 )。但实际上它代表的是 。
-
在 的表示法中: 被表示为 。 它的绝对值是 ,这非常小,远小于 。这正确地反映了噪声的物理性质。
数学上的解释
- 同态加密的本质是模运算: 意味着 和 在环上是同一个元素。
- Shortest Representative(最短代表元): 当我们需要衡量一个元素的大小(范数 )时,我们必须选择它在同余类中绝对值最小的那个代表元。
- 对称区间的优势: 区间 天然地包含了所有模元素的“最短代表元”。在这个区间里,数值的绝对值直接对应于它在晶格(Lattice)中离原点的距离(即噪声大小)。
总结: 选 是为了让数值的绝对值直接等同于噪声的大小。如果你用 ,你就需要额外一步逻辑:“如果 ,则实际大小是 ”。用对称区间可以省去这个麻烦,且符合误差分布(通常是高斯分布,均值为 0)的直觉。
2. 关于 Gadget Decomposition
这是一个在全同态加密(FHE)中非常经典的技术,主要用于优化 Key Switching (密钥切换) 操作。
2.1 为什么 Gadget decomposition 能够减少模数消耗?
首先要明白如果不做 Decomposition,Key Switching 有多“费模数”。
Key Switching 的痛点: 假设我们有一个密文 (系数很大,接近 ),我们需要把它乘以一个密钥转换公钥 (也很大,接近 )。 直接相乘 会得到一个巨大的数,其大小约为 。
- 这里面的噪声也会被放大 倍(即 )。
- 为了消除这个巨大的噪声,标准做法是除以一个巨大的辅助模数 (Modulus Switching / Rescaling)。
- 模数消耗: 这意味着你必须在系统参数里预留一个巨大的 (通常 )。这会占用你的总模数预算(Total Modulus Budget)。你的 必须很大,导致安全性下降或参数变大。
Gadget Decomposition 的魔法: 它把大数 拆成了一堆小数 。 其中每个 都很小(小于基数 )。
然后,我们不直接乘 ,而是把 也拆成针对每一位的“小公钥”向量: 其中 是针对 这一位的加密。
计算变成了:
为什么省模数?
- 噪声变小了: 现在的噪声不再是 ,而是 (因为 很小)。
- 不需要大 : 因为噪声增幅很小(只是乘以了 ),我们就不需要除以一个巨大的 来压制噪声。
- 结论: 我们省下了那个巨大的辅助模数 的空间,或者说让 可以变得很小。这就叫做“减少了模数消耗”。
2.2 三种 Gadget Decomposition 的具体做法
这三种方法的本质区别在于**“基数(Base)”**的选择。假设我们要分解大整数 。
1. Bit Decomposition (位分解)
- 做法: 把 变成二进制形式。基数 。 其中 。
- 特点:
- 优点: 噪声最小(因为系数是 0 或 1)。
- 缺点: 分解出来的项数最多( 项)。导致 Key Switching Key 的尺寸非常大(因为每一位都要对应一个 Key),计算也最慢。
2. Digit Decomposition (数字/字分解)
- 做法: 选择一个较大的基数 (例如 或 )。 其中 。
- 特点:
- 平衡点: 这是最常用的方法。
- 基数 越大,项数越少(Key 越小,速度越快),但噪声越大(噪声 )。
- 基数 越小,项数越多,但噪声越小。
- CKKS 的各个库(如 SEAL, HEaaN)通常默认使用这种,通过调整 (论文里的 )来平衡性能和噪声。
3. RNS Decomposition (基于剩余数系统的分解)
- 背景: 在实际代码中,大整数 是由一串小质数 的乘积构成的。大数 是以 RNS 形式存储的:,其中 。
- 做法: 并不是把 RNS 直接当作 Digit。RNS 分解通常结合 CRT(中国剩余定理)。
- 它将 视为 的形式(类似 CRT 重建公式)。
- 在 Key Switching 时,利用 RNS 的正交性质,将计算分散在每个小模数 上独立进行。
- 特点:
- 这是工程实现上最快的方法,因为它避免了大整数的高精度运算(BigInt arithmetic),所有操作都在 64 位机器字长内完成。
- 它是现代同态加密库(如 Microsoft SEAL, PALISADE/OpenFHE)的标准实现方式。
总结表格:
| 分解类型 | 基数 | 系数大小 | Key 大小 | 噪声增长 | 备注 |
|---|---|---|---|---|---|
| Bit | 2 | 最大 | 极小 | 理论常用,太慢 | |
| Digit | (如 ) | 中等 | 中等 () | 灵活可调 | |
| RNS | 质数 | 较小 | 较小 | 工程标准,利于并行 |
BOB:2.3 CKKS bootstrapping详细解释
这一节(2.3 CKKS bootstrapping)介绍了 CKKS 方案中至关重要但代价昂贵的**“自举”(Bootstrapping, BTS)**过程。
为了让你彻底理解,我将通过**“为什么需要它”、“它的核心难点是什么”以及“具体四个步骤的逻辑”**三个层面来详细解释。
1. 为什么需要自举?(背景)
在 CKKS 中,每一次乘法运算后,为了维持密文的比例因子(Scaling Factor)不爆炸,我们必须执行 Rescale 操作。
- Rescale 的代价: 每次 Rescale 都会消耗掉一层模数(比如从 降到 )。
- 后果: 随着计算层数增加,模数越来越小,最终会降到底层模数 。此时,模数耗尽,无法再进行任何乘法运算。
- 自举的作用: 就像给电池充电一样。它接收一个模数即将耗尽的密文(在 下),把它变成一个拥有大模数()的新密文,同时里面的明文消息 保持不变(或者只增加很少的噪声)。这样计算就可以无限进行下去。
2. 核心难点:那个“幽灵”整数
自举最难的地方在于:模数转换不是线性的。
-
在小模数 下,密文 满足: 这意味着在数学上: 其中 是某个整数多项式(也就是同余式里的那个 )。在模 的世界里, 是 0,所以看不见。
-
当我们强行把模数提升到 (ModRaise)时: 我们直接把 的系数看作是 空间里的元素。 此时,解密这个新密文: 因为 很大(远大于 ),所以这一项 不再是 0 了!它变成了一个巨大的误差项,完全掩盖了原本的消息 。
-
自举的任务: 就是要在加密状态下,把这个巨大的 算出来并减掉,只留下 。这等价于计算 “模 约减” 函数。
3. 四个步骤详细解析
论文中提到的四个步骤(StC, ModRaise, CtS, EvalMod)是为了解决上述问题而设计的流水线。
步骤 1 & 3: StC 和 CtS (线性变换)
这是**系数域(Coefficients)和槽域(Slots)**之间的搬运工。
- 背景:
- ModRaise 产生的误差 是存在于多项式系数中的。
- EvalMod(去处误差)需要做大量的多项式乘法。在 CKKS 中,乘法在 Slots(槽) 模式下(SIMD)效率最高,而在系数模式下做多项式乘法非常慢(卷积)。
- CtS (Coeff-to-Slot):
- 将多项式的系数提取出来,搬运到槽里面去。
- 本质上是一个同态 DFT(离散傅里叶变换) 或者是其变体。
- 它包含大量的旋转(Rotation)和常数乘法。
- StC (Slot-to-Coeff):
- 是 CtS 的逆过程,把处理好的数据放回系数里。
(注:具体的顺序取决于实现,通常是 ModRaise -> CtS -> EvalMod -> StC,或者 StC -> ModRaise -> EvalMod -> CtS,核心目的是为了在最合适的域做 EvalMod)
步骤 2: ModRaise (模数提升)
这是最简单粗暴的一步,也是引入问题的源头。
- 操作: 简单地将定义在 上的密文 ,视为 上的多项式。
- 结果: 密文现在的模数变大了(有了做运算的资本),但是它**“脏了”**。解密它会得到 。我们需要在下一步把 洗掉。
步骤 3: EvalMod (同态模约减)
这是最核心、最耗时的一步。
- 目标: 给定输入 ,我们需要计算 。
- 数学问题: 模运算 是一个锯齿波函数,它是非连续、非线性的。同态加密只能做加法和乘法(即多项式)。
- 解决方案: 使用多项式来逼近这个模运算函数。
- 通常使用泰勒级数、切比雪夫多项式,或者基于正弦函数的组合(因为 具有周期性,很像模运算)。
- 例如:近似计算 (针对 较小的情况)。
- 代价: 计算这种高次多项式需要消耗大量的乘法深度。这正是为什么自举本身就会消耗大量模数的原因。
4. 总结:自举的全过程逻辑
- ModRaise: 强行提升模数,导致密文里混入了大整数倍的 (即 )。
- CtS(变换): 为了方便计算,把这些混杂了误差的系数搬运到 SIMD 的槽里。
- EvalMod(清洗): 在槽里跑一个高次多项式,模拟“取模”操作,把 去掉,只剩下 。
- StC(归位): 把洗干净的数据搬回多项式系数里,得到最终干净的、大模数的新密文。
论文的切入点
作者在这里详细介绍自举是因为:
- 自举虽然好,但是太贵了(EvalMod 和线性变换都很慢且消耗模数)。
- Mult² 的优势: 通过节省乘法的模数消耗,可以让用户推迟自举的时刻(跑更深再自举),或者在某些情况下完全避免自举。这直接提升了同态加密的实用性。
BOB:在3.2 Pair representation中: Definition 3.3. Let Ql be an element of the modulus chain 这句话中的Ql应该是l个素数的乘积?
不完全准确。准确地说,应该是 个素数的乘积。
根据论文 第 4 页(2 PRELIMINARIES) 中对 Residue number system (RNS) 的定义:
“Let be a set of primes and .”
这就意味着 是从下标 到下标 的所有素数相乘。
让我们详细拆解一下:
-
索引是从 0 开始的:
- 。
- 总个数是 个。
-
物理含义:
- (Base Prime): 这是最底层的素数,通常用于最后的解密和编码,必须保留到最后。
- (Level Primes): 这些是用来支持 层乘法的“燃料”。每做一次 Rescaling,就会消耗掉最上面的一个素数。
-
在 Definition 3.3 中的语境:
- 当定义说 时,它指的是**“当前密文处于第 层”**。
- 这意味着这个密文还可以支持 次标准的 CKKS 乘法(或者在 语境下,通过组合可以支持更多)。
- 它的模数大小(Bit-size)大约是:。
总结: 包含 1 个基础素数 () 加上 个乘法素数 (),合计 个素数。
BOB:对于定义3.1,其ct密文的表示并不是在RNS下的? 那为什么3.3中的ct密文又是在RNS下了?
这是一个关于论文理论抽象与工程实现之间如何衔接的极好问题。
简单直接的回答是:Definition 3.1 是纯数学层面的抽象定义(不关心底层表示),而 Definition 3.3 是将这个数学定义应用到 CKKS 模数链体系中的具体配置(这就隐含了 RNS 结构)。
我来为你详细拆解其中的逻辑转换:
1. Definition 3.1:抽象的数学操作
问题: “对于定义 3.1, 其 ct 密文的表示并不是在 RNS 下的?”
回答: Definition 3.1 是“表示中立”(Representation-agnostic)的。
- 数学抽象: 在 Definition 3.1 中,作者使用的是环 。这里的 只是一个代数上的大整数。公式: 这些公式描述的是**“我们要对多项式做什么”,而不是“计算机内存里怎么存这些多项式”**。
- 无论你用什么表示: 无论你是用一个巨大的数组存大整数(BigInt),还是用 RNS 存一堆小整数,Definition 3.1 的数学含义是不变的——就是做带余除法。
- 为什么看起来不像 RNS? 因为如果 只是一个随意的整数,而在 RNS 系统下要计算 是非常困难的(需要复杂的 RNS 转换算法)。作者为了定义的通用性和简洁性,这里不提 RNS,只谈数学性质。
2. Definition 3.3:结合 CKKS 模数链(隐含 RNS)
问题: “那为什么 3.3 中的 ct 密文又是在 RNS 下了?”
回答: 因为 Definition 3.3 将上述数学定义“实例化”到了 CKKS 的上下文里,而 CKKS 的模数链 本质上就是 RNS 结构的。
- 引入上下文: Definition 3.3 提到了 “Let be an element of the modulus chain”。
- 在 CKKS 中,模数链 。这本身就暗示了 RNS 的存在。
- 构造特殊的模数: 这里定义了 。
- 在 第 6 章 (Experiments) 和实现细节中,作者明确指出 被选为 RNS 基中的一个素数(或者是素数的乘积)。
3. 关键点:当 3.1 遇见 3.3(RNS 技巧)
这才是你感到困惑的核心——作者是如何把“难算的 3.1”变成“好算的 3.3”的?
当我们将 Definition 3.1 应用于 RNS 形式的密文,并且巧妙地选择除数 为 RNS 的其中一个模数时,奇迹发生了:
-
对于 (取余):
- 在 RNS 中,密文被表示为 。
- 如果我们想求 ,在 RNS 里这不需要任何计算!直接把对应 的那个分量拿出来就行了。
- 这就是为什么在 3.3 的语境下,操作变得极其高效。
-
对于 (取商):
- 公式是 。
- 在 RNS 中,这等价于**Rescaling(重缩放)**操作:扔掉 对应的分量,然后在其他分量上乘以 。
- 这正是 CKKS 标准的 RNS-Rescaling 算法。
总结
- Definition 3.1 (What to do): 无论底层怎么存,我都要把密文 拆成 。这是纯数学定义。
- Definition 3.3 (How to do it efficiently): 在 CKKS 模数链中,我们专门加了一个 RNS 素数叫 。此时,3.1 定义的“取余”变成了“取分量”,3.1 定义的“取商”变成了“Rescaling”。
所以,并没有矛盾。3.1 是通用的数学描述,3.3 是基于 RNS 架构的高效实现配置。
BOB:Before introducing our algorithm, we recall a classical technique used to double precision in fixed-point arithmetic.
这里的fixed-point arithmetic是什么东西?
Fixed-point arithmetic(定点数算术/定点运算) 是一种在计算机中表示和计算小数(实数)的方法。
简单来说,它的核心思想是:把小数放大成整数来存,计算完再缩小回去。
为了让你完全理解这句“classical technique”,我们需要拆解一下定点数的原理以及它和这篇论文的关系。
1. 什么是定点数(Fixed-Point)?
计算机里通常只擅长处理整数。为了处理小数(比如 ),有两种主流方法:浮点数(Floating-point)和定点数(Fixed-point)。
- 浮点数(大家熟悉的): 小数点是“浮动”的。比如 和 。它能表示极大的数和极小的数,但硬件实现复杂。
- 定点数(CKKS 用的): 小数点的位置是固定的。我们约定好,所有的数都放大了 倍(或者是 倍)。
通俗例子:钞票
想象一下,你不想处理“12.34 元”这样的小数。 你决定:所有的钱都以“分”为单位(Fixed-point)。
- 表示: “12.34 元” 你存储为整数 1234(分)。
- 约定: 这里的“缩放因子”是 100。大家都知道,拿到这个整数后,小数点默认要往左移两位。
这就是定点数算术:用整数运算模拟小数运算。
2. 为什么论文提到“经典技术”?
论文中说:“recall a classical technique used to double precision…”(回顾一种在定点算术中用于双倍精度的经典技术)。
这个“经典技术”指的是:当数字太大,寄存器装不下时,如何把大数拆成两半来做乘法。
场景还原
假设你的计算器(或 CPU)很老旧,它只能做 2 位数的乘法(比如 ),如果结果超过 4 位数就会溢出。 现在你需要计算两个 4 位数 的乘法:。怎么做?
经典技术(拆分法): 你把数字拆成 高位(High) 和 低位(Low)。 设定拆分点(基数) 。
- (高位 12,低位 34)
- (高位 56,低位 78)
现在计算 :
展开这个式子(分配律):
这有什么用? 这里的每一次小乘法(比如 )都是 2 位数乘法,你的老旧计算器完全算得过来!算完之后,再通过移位(乘以 10000 或 100)和加法把结果拼起来。
这就是论文的核心灵感:
- CKKS 的模数 有限,就像那个“只能算 2 位数的计算器”。
- 为了算更高精度的数,论文使用了这个“经典定点数拆分技术”,把大密文拆成了 。
- 区别在于,论文为了省模数,故意扔掉了最后那一项 。
3. 定点数与 CKKS 的关系
CKKS 本质上就是一个定点数加密系统。
- Scaling Factor (): 这就是定点数的缩放因子。
- Encoding: 把实数 变成整数 。
- Rescaling: 就像定点数乘法后通常需要除以缩放因子一样。
- 比如“分”乘“分”: —— 没问题。
- 但是 ?
- 物理意义上变成了“平方分”。数值变成了 。
- 为了变回“分”,你必须除以 100。
- 这就对应 CKKS 的 Rescaling(除以 )。
总结: 文中提到的“fixed-point arithmetic”指的就是这种通过放大因子用整数模拟小数的机制。而那句“classical technique”指的是将大整数拆分为高低位进行分块乘法的算法,这正是 算法的原型。
BOB:在RNS-CKKS下,密文的解密是怎样的?假设在l层进行解密,那么ct_l和sk进行内积,得到的不是一个长度为l的向量吗?解密消息在哪里?
这是一个非常棒的问题!你敏锐地察觉到了 RNS(剩余数系统)表示法 和我们直觉中的 大整数/多项式 之间的“视觉差异”。
简单回答你的问题: 是的,内积的结果确实是一个“向量”(或者说是一组小整数的列表)。 但是,这个向量整体“就是”那个解密后的消息多项式。你之所以没看到“消息”,是因为它还穿着 RNS 的“马甲”。
为了拿到真正的明文消息,你需要进行最后一步操作:CRT 组合(Chinese Remainder Theorem Reconstruction)。
我为你详细拆解这个过程:
1. 解密的第一步:RNS 域内的内积
假设我们在第 层解密。
- 模数: (大模数)。
- 密文 : 在 RNS 下,它由两部分多项式 组成。而每个多项式的系数都分别存储在 个小模数 下。
- 实际上是列表:。
- 实际上是列表:。
- 私钥 : 也是以 RNS 形式存储的:。
执行内积 : 这个操作是**分量并行(Component-wise)**进行的。对于每一个 RNS 分量 (从 到 ),我们计算:
结果: 你确实得到了一个长度为 的向量(列表):
这里的每一个 都是一个多项式,但它的系数都很小(在 范围内)。
2. 消息在哪里?(CRT 重建)
这时候你可能会问:“我的消息 在哪?是 吗?还是 ?” 都不是,也都是。
这就像我问你:“数字 10 在哪里?” 如果我们在 RNS 基 下表示 10:
- 表示形式是向量 。
数字 10 既不是 1,也不是 0,而是 (1, 0) 这一对数所唯一确定的那个大整数。
CKKS 的情况同理: 真正的解密后多项式 (也就是 ),是一个系数巨大的多项式。 上述向量 就是这个巨大多项式 在模 下的 RNS 表示。
为了看到“消息”,你需要做 CRT 重建(CRT Composition): 利用中国剩余定理公式,把这些小多项式拼回去:
- 这一步算完后,你就得到了一个大整数多项式 。
3. 解密的最后一步:解码(Decode)
现在你手上有了一个大整数多项式 。 它的物理意义是:
接下来的步骤(通常在 CPU 的大数库或浮点库中完成):
- 系数转换: 把 的系数从模 域()映射到有符号整数域()。
- 除以缩放因子: 每个系数除以 。
- Canonical Embedding 逆变换: 把这个多项式 映射回由复数组成的向量(Slots)。
这就是你最终看到的明文消息。
总结
- 你的直觉是对的: 内积的结果就是一个 RNS 向量。
- 消息在哪里: 消息并没有“躲”在向量的某一位里,整个向量合起来才是消息。
- 如何提取:
- 内积(在 RNS 域并行完成,得到一串小余数)。
- CRT 重建(把小余数拼成大整数多项式)。
- 除以 (把整数变回浮点数)。
(注:在高效的代码实现如 HEaaN/SEAL 中,为了速度,步骤 2 和 3 往往是合并优化的,直接通过算法从 RNS 转换到浮点数,而不显式生成那个巨大的 BigInt 多项式,但逻辑原理就是上面这样。)
BOB:4.1 Tools的 Lemma 4.2 ,我没看懂,向我 详细解释
Lemma 4.2 是整篇论文中 算法的数学基石。
它主要证明了两件事:
- 正确性: 我们定义的 运算(扔掉低位乘低位),在数学上确实等价于把两个大密文相乘后除以了 。
- 误差可控: 那个被我们扔掉的项(低位 低位),不仅是可以被忽略的,而且它的具体的误差形式是非常清晰的。
我来一步步为你拆解这个引理的推导过程。
1. 符号与背景设定
首先,我们先把复杂的符号简化一下,方便理解:
-
输入: 两个密文对 和 。
- 对应的大数是 。
- 对应的大数是 。 (注:这里 是高位, 是低位)
-
目标: 我们想计算 。
-
代数展开(标准乘法): 展开这个括号: 这是完全正确、没有损失的数学真理。
2. 做了什么?
论文中定义的 操作生成了一个新的密文对 :
- 新高位: (对应 )。
- 新低位: (对应 )。
- 扔掉的项: 被丢弃了。
现在,我们把这个 的结果**重组(RCB)**回去看看它代表什么数:
3. Lemma 4.2 的核心等式解析
Lemma 4.2 的第一个公式本质上就是把 “标准乘法” 和 “ 乘法” 放在一起比较。
我们把上面的“标准乘法展开式”变形一下:
仔细看中括号里的内容,那正是 !
所以,就得到了 Lemma 4.2 的核心逻辑等式:
对应论文中的公式: (注:乘 是因为 Tensor 后密文变成了 3 维,需要用 解密)
这个等式告诉我们两件事:
- 隐式除法: 的结果,大约等于 。这就解释了为什么我说它自带“隐式除法”功能。
- 误差来源: 剩下的误差项就是 (即论文中的 )。
4. 误差界限(Bound)解析
Lemma 4.2 的后半部分是在算:这个被扔掉的误差到底有多大?
论文给出的界限是:
我们来推导一下为什么是除以 :
-
绝对误差: 被扔掉的项是 。
- 的大小约为 。
- 所以绝对误差约为 。
-
相对误差(归一化):
- 请注意, 的输出结果(即那个商)是处于被“除以了 ”的尺度上的。
- 为了衡量误差对结果的影响,我们必须把绝对误差也除以 。
- 想象一下:原本误差是 100。但因为你的结果缩小了 100 倍,所以相对于结果来说,这个误差相当于只剩 1 了。
-
结论: 所以,最终对解密结果的影响(Infinity Norm)被控制在 这个量级。
- 只要我们选的 足够大(比 大),这个误差就会小于 1,从而被忽略不计。
总结
Lemma 4.2 是在用数学语言说:
“兄弟们,我们把 这些项算出来,拼成一个新的密文。虽然我们扔掉了 这一项,但根据公式推导,我们得到的新密文,在数学上严格等于 ‘(原数乘积 - 扔掉的垃圾) 除以 ’。只要垃圾足够小,我们算出来的就是对的,而且还顺便帮大家做了一次免费的除法!”
BOB:为什么要保证这个条件?以及这个条件是怎么推导出来的?
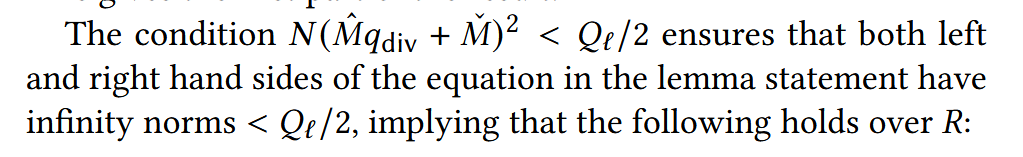
这是一个非常核心的问题,涉及到同态加密中**“模运算正确性”**的边界条件。
简单来说,这个条件是为了保证**“计算结果没有发生溢出(Wrap-around)”**。如果结果溢出了模数 ,那么原本在整数环 上成立的等式,在模 的密文空间里就不再成立了。
我来为你详细拆解这个条件的推导过程和背后的逻辑。
1. 为什么要保证这个条件?(防止溢出)
核心逻辑: Lemma 4.2 试图证明一个等式: 这个等式是在 整数多项式环 上讨论的(即没有取模)。
然而,CKKS 的密文是存储在 模 的环上的。
- 左边(Standard Tensor): 计算的是两个密文的乘积,解密后对应明文 。
- 如果 的数值非常大,超过了 ,系统就会发生取模回绕。
- 比如:模数是 100,计算结果是 120。在密文里它变成了 20。
- 但是右边的数学推导是基于“结果是 120”进行的。
- 后果: 。等式在模 下失效了。
结论: 必须保证乘法结果的**绝对值(范数)**始终小于 ,这样模运算的结果才等于真值,引理中的数学推导才能在密文世界里生效。
2. 这个条件是怎么推导出来的?
让我们像剥洋葱一样拆解公式:
第一步:估算单个明文的大小
我们在做乘法 。先看 有多大。 根据分解定义:
- 是高位(商),其大小(范数)有界限 。
- 是低位(余数),其大小(范数)有界限 。
- 是放大的倍数。
根据三角不等式,明文 的最大范数大约是:
第二步:估算乘积的大小
现在计算两个这样的明文相乘:。
在多项式环 中,两个多项式相乘,其系数会发生膨胀。 膨胀公式: 如果 且 ,那么 。 (注:这里 是多项式的度,比如 。这是因为卷积运算会把 个项累加起来)
将第一步的界限代入:
第三步:限制在模数范围内
为了保证计算 时不发生模 的溢出,这个乘积的范数必须小于模数的一半:
即:
3. 物理意义解读
这个公式实际上是在告诉我们:当前的模数 是否足够大,能够容纳得下这次乘法的结果?
- : 这是明文的主要部分(数值本身)。
- 平方: 因为做了乘法,数值规模平方了。
- : 多项式乘法带来的系数膨胀。
- : 容器的大小。
如果这个条件不满足,说明模数太小了(或者明文太大了),乘法结果把容器撑爆了。这就意味着我们在做 这一步时,还没来得及做 Rescaling,数据就已经损坏了。
所以,这是一个安全性检查(Sanity Check),确保在执行 的第一步(Tensor)时,基础的 CKKS 乘法逻辑是成立的。
BOB:这个图中的left and right hand sides of the eqution指的是什么
这张图里提到的“equation in the lemma statement”(引理声明中的等式),指的就是 Lemma 4.2 中给出的那个核心等式。
为了让你看清楚,我把 Lemma 4.2 中的那个等式写出来(对应论文第 7 页):
这里的 Left and Right 分别指代:
1. Left Hand Side (LHS): 标准乘法的解密值
- 物理含义: 这是标准 CKKS 乘法(Tensor)得到的结果的解密值。
- 数值大小: 它代表了两个明文的直接乘积 。
- 估算:
- 所以 LHS 的大小约为 (再乘上多项式膨胀系数 )。
2. Right Hand Side (RHS): 分解乘法的重组值
- 物理含义: 这是通过 算法(Tensor)算出来的结果,乘以 后,再加上那个被扔掉的“低位 低位”误差项。
- 数值大小: 在数学上,它应该严格等于 LHS。所以它的大小也约为 。
这里的逻辑链条
-
原本的等式是“模 同余”: Lemma 4.2 最初只说左右两边在 下是相等的。
-
我们需要的是“真相等”: 为了证明误差分析是正确的,我们需要这个等式在整数环 上直接成立(即 ,而不仅仅是 )。这对于后续把 除过去至关重要。
-
条件的作用: 图中提到的条件 就是在说:
“大家看,LHS(也就是 )的最大可能值都比模数的一半要小。”
- 既然 LHS (没有溢出)。
- 且 RHS 在数学上等于 LHS。
- 那么 RHS (也没有溢出)。
- 结论: 既然两边都没溢出,且模 相等,那它们就是真的相等(holds over )。
总结: Left/Right Hand Sides 指的就是 “明文真值(LHS)” 和 “算法算出来的还原值(RHS)”。这句话是在确保这两个值都没有因为太大而撑爆模数容器。
BOB:Lemma 4.4.中的这段话是啥意思?

这段话是在解释为什么作者设计的 算法比一种“直观但幼稚”的方法更优秀。
核心争论点在于:做一次重线性化(Relinearization),到底会不会让你的密文模数变小(即“消耗模数”)?
我为你拆解这段话的逻辑:
1. 那个“幼稚的方法” (The Naive Approach) 是什么?
逻辑是这样的:既然我们已经把密文拆成了 ,那我们要对它做 Relin,最简单的思路不就是:
- 拼回去 (RCB): 先把两部分合体,变回一个大密文 。
- 做标准 Relin: 对这个大密文做普通的 CKKS 重线性化。
- 再拆开 (DCP): 把做完的结果再拆成新的 。
即公式:。
2. 为什么幼稚的方法会“消耗模数”?
作者指出:“Note that this consumes modulus… DCP decreases the modulus”。
- RCB 和 Relin 阶段: 密文模数保持在 。
- DCP 阶段(问题的关键):
- DCP 的功能是把一个密文 拆成商和余数。
- 为了得到“商”(),我们实际上是在做 。
- 在 RNS-CKKS 中,除法操作(Rescaling)是必须通过“丢弃一个模数”来实现的。
- 所以,当你执行 DCP 时,你必须扔掉 这一层的模数。
- 结果: 你的密文模数从 变成了 。你亏了一层模数!
3. 作者的方法 () 为什么“不消耗模数”?
作者的策略是:先乘后除,抵消损耗。
回顾 的公式第一项:
这里的操作流程是:
-
预先放大 (Multiply by ):
- 作者没有直接对 做 Relin,而是先把它乘了 。
- 在代数上,这意味着这个多项式的数值扩大了 倍。
- 在模数意义上,你可以理解为我们虚拟地把它提升到了一个更大的模数空间(或者是把原本属于 这一层的“配额”给补上了)。
-
执行 DCP (Divide by ):
- DCP 操作虽然会物理上“消耗”掉 这个模数因子(执行除法)。
- 但是! 因为我们第一步已经先乘了 。
- 所以:(原模数 ) 原模数。
4. 总结这段话的意思
- 幼稚做法: 是“裸奔”。直接去分解(做除法),导致模数真的变小了。
- (亏了)。
- 作者做法: 是“带资进组”。先乘一个 进去,再分解(除以 )。
- (没亏)。
结论: 这段话在吹嘘 的设计巧妙之处:它通过数学上的预处理,使得这一步操作变成了**“模数免费”**的操作,从而把宝贵的模数节省下来留给 Rescaling()步骤使用。
BOB:对ct^乘以q_div要怎么实现?
这是一个非常切中要害的工程实现问题!
在 RNS-CKKS 的架构下,实现“将密文 乘以 ” 实际上是一个**“模数提升(Modulus Raising)”的特例,而且是一个非常简单且计算代价极低**的特例。
我们假设当前的 处于模数 下,RNS 基为 。 我们的目标是获得一个处于模数 下的新密文。
具体实现步骤如下:
1. 对现有的 RNS 分量:标量乘法
对于当前已经在 中的每一个 RNS 模数 ():
- 我们直接执行多项式系数的标量乘法。
- 计算公式:
- 工程细节: 是一个常数整数。这一步就是把多项式的每个系数都乘以这个常数。
2. 对 分量:直接置零(关键步骤)
既然我们要把模数扩充到包含 ,我们需要确定新密文在 这个模数下的 RNS 分量是多少。
- 数学逻辑: 我们正在计算 。
- 模运算: 任何数乘以 后,再对 取模,结果必然是 0。
- 工程实现: 你不需要做任何复杂的 RNS 基转换(Basis Extension)。你只需要添加一个新的 RNS 分量(对应 ),并将该分量的所有多项式系数直接设为 0。
为什么说这“不消耗模数”?
结合上述实现,我们再看回头看 的全过程:
-
乘 (Raise Modulus):
- 现有分量乘以常数。
- 新增一个 分量,填 0。
- 状态: 密文现在拥有了 的模数空间。
-
做 Relin(Key Switching):
- Key Switching 通常需要产生大模数密文,并在最后进行除法(Rescale)。
- 在这个扩充后的模数空间里做 Relin。
-
做 DCP(分解/除法):
- DCP 的本质是“Rescaling by ”。
- 操作: 扔掉 这个 RNS 分量(刚才那个 0 分量,或者经过 Relin 变成非 0 的分量),然后把其他分量乘以 。
- 状态: 密文回到了 的模数空间。
总结: 实现“乘以 ”之所以简单且高效,是因为它是正好乘以模数本身。在 RNS 系统中,这等价于**“在原基础上乘常数” + “在扩展位上填 0”**。这避免了常规模数提升(Modulus Switching Up)中极其昂贵的通用基转换计算。
BOB:我有个疑问,在这篇论文的实现里,素数模数是不是比一般的rns-ckks中的素数模数小一半?然后模数数量要多一倍?
这是一个非常敏锐的观察!你的直觉触及到了工程实现的核心,但实际情况和你推测的刚好相反。
简短的回答是:
- 素数模数的大小(Bit-size): 并没有变小一半,它们保持不变(通常都是 50~60 bits,为了适配 64 位机器字长)。
- 模数的数量(Number of primes): 并不是多一倍,而是少了一倍(对于同等精度的每一层乘法而言)。
让我用论文中的 100-bit 高精度 案例(Table 3)来为你详细拆解这笔账。
1. 为什么素数模数大小不变?
在 RNS-CKKS 的工程实现(如 HEaaN, SEAL)中,为了追求 CPU 运算速度,每一个 RNS 素数 都必须小于 64 bits(通常选 50-60 bits)。这样所有的模运算都可以直接用 CPU 指令完成,不需要调用慢速的大数库。
- 标准 CKKS: 只能用 60-bit 以下的素数。
- Mult: 也只能用 60-bit 以下的素数。
- 结论: 单个素数的大小是物理硬件决定的,大家都一样。
2. 怎么实现 100-bit 精度?(Standard vs Mult)
假设我们的目标是 Scaling Factor (即每次乘法后需要除以 )。
A. 标准 CKKS 的做法(“拼单”)
因为一个素数最大只有 60 bits,凑不够 100 bits。 所以,标准 CKKS 必须用两个素数来凑一层。
- 它会定义 。
- 比如 。
- 每次 Rescaling,要同时扔掉 和 这两个素数。
- 消耗: 每层消耗 2 个 RNS 素数。
B. Mult 的做法(“单干”)
Mult 的魔法在于:它只需要“物理消耗”一半的模数(即 ),另一半()通过算法结构“白嫖”了。
- 它需要的物理模数 只需要 50 bits。
- 这正好这就是一个标准的 RNS 素数的大小。
- 消耗: 每层只消耗 1 个 RNS 素数。
3. 最终对比:谁用的模数更多?
让我们看论文 Table 3 的实验数据(针对 8 层乘法,100-bit 精度):
| 特性 | 标准 CKKS (Standard) | Mult (Our work) |
|---|---|---|
| 单层所需的模数位宽 | 100 bits | 50 bits |
| 素数配置 (RNS Primes) | (50 × 2) (每层需要 2 个 50-bit 素数拼起来) | 60 × 1 (每层只需要 1 个 60-bit 素数) |
| 8 层所需的素数总数 | 个 | 个 |
| 最大总模数 () | 1000 bits | 680 bits |
(注:680 bits 中包含了基础模数和其他开销,所以不是简单的 ,但明显远小于 1000)
结论
你的推测逻辑是:“如果要省一半模数,是不是因为把模数切小了?”
事实是: 模数块(积木)的大小没变(都是 50-60 bit 的标准砖头)。
- 标准 CKKS 盖一层楼需要 2 块砖(为了凑 100 高度)。
- Mult 盖一层楼只需要 1 块砖(它自带 50 的虚拟高度)。
所以,Mult 实际上是大幅减少了模数的数量和总大小,这正是它能提升速度和减小密文尺寸的根本原因。
BOB: 但是密文的数量加倍了,对吧? 以及q_div的大小和素数模数的大小相加应该等于scale?
你的这两个理解都非常准确!
你已经完全看透了这篇论文在“宏观架构”和“参数微观搭配”上的核心逻辑。
1. 关于“密文数量加倍”
是的,逻辑上密文数量确实加倍了。
- 逻辑结构: 在 算法中,我们在内存中维护的对象不再是一个单独的 ,而是一个密文对(Ciphertext Pair) 。
- 组件数量:
- 标准 CKKS:1 个密文(包含 2 个多项式 )。
- :2 个密文(包含 4 个多项式 )。
但是!为什么论文还说它能减小密文大小(Storage Size)呢?
这是因为虽然“数量”翻倍了,但每个“单体”变轻了很多。这里有一个**“以数量换空间”**的博弈:
- 模数变小():
- 标准密文的模数 bits。
- 密文的模数 bits。
- 单体变小了约 30%。
- 环维数减半(): 这是最关键的!
- 因为模数变小了,根据 LWE 安全性估算,我们可以把环维数 从 降到 。
- 这直接让多项式的系数个数少了一半。
总账计算(以 Table 3 为例):
- 标准 CKKS: bits。
- Mult: bits。
结论: 虽然我们手里拿了两个密文,但因为每个密文都变得非常“袖珍”(维度减半、模数减小),所以总的存储空间反而变小了(从 14.8MB 降到了 5.08MB)。
2. 关于“ 和素数模数的大小相加等于 Scale”
完全正确! (准确地说是比特数(Bit-size)相加)。
这里的数学关系是乘法关系,但在工程参数(Bit-size)上表现为加法关系。
- 总目标(Scale): 我们希望维持的总缩放因子是 (即 100 bits)。
- 你的公式:
- 对应数值:
物理意义的对应:
-
(约 50 bits):
- 这是**“隐式 Scaling”**。
- 在 步骤中,通过扔掉低位和提取高位,数据在数学上被缩小了 倍。
- 这部分缩放是不消耗模数链的。
-
(约 50 bits):
- 这是**“显式 Scaling”**。
- 在 步骤中,通过物理除法,数据被缩小了 倍。
- 这部分缩放是消耗模数链的(也就是我们实打实用的那个 RNS 素数)。
总结: 你理解得非常透彻。 本质上就是把一个大的 Scaling Factor(比如 100 bits)拆成了两半:
- 一半(50 bits)塞给 用算法结构去“白嫖”。
- 一半(50 bits)塞给 用物理模数去“支付”。 这就解释了为什么模数消耗减半了。
BOB:4.2的Modulus consumption.中,为什么the size of Mˇ是C ^ 2 * q_div?
这是一个非常细致的问题!你可能是在阅读论文第 8 页 Modulus consumption 这一段时,对其中的公式推导产生了疑惑。
实际上,这里存在一个阅读上的陷阱(或者是论文原文的一个笔误/简写)。
准确地说: 的大小(Size)应该是 ,而不是 。
那个出现的 其实是误差项公式计算后的结果。
我来为你详细还原这个推导过程:
1. 的真实定义
首先, 是低位部分(Low Part) 的范数上界。 根据分解的定义(Decomposition): 也就是 除以 的余数。
在数学上,余数绝对不能超过除数。所以: 因此,我们可以认为 的大小主要由 决定。 我们可以记作: (其中 是一个接近 或稍大一点的常数,考虑到噪声增长)。
2. 为什么出现了 ?
这个项出现在误差项的计算中。
回顾 Theorem 4.8 和 Lemma 4.2, 引入的主要误差项是: (注:这里忽略了多项式膨胀系数 和分母中的 )
让我们把 代入这个公式:
真相大白: 文中提到的 并不是 本身的大小,而是** 除以 之后得到的结果**。
3. 结合论文原文的解析
论文原文写道:
“In order to keep the main component small…” (原文这里可能有笔误,应该是 而不是 ,根据 Lemma 4.2 的结论)
这里的逻辑链是:
- 前提: 假设 。
- 公式: 主要误差源是 。
- 代入: 分子变成了 。
- 约分: 分子的 和分母的 约掉一个。
- 结果: 剩下 在分子上。
总结
- 的大小 是 (线性的)。
- 是误差项(也就是 )简化后的数值。
- 这也再次验证了我们之前的结论:为了让误差 小于 1,我们必须要求 。
BOB:
4.2的结尾:
为什么Tensor步骤不需要NTT?

这是一个关于同态加密工程实现的经典问题。
简单直接的回答是:因为在高效的同态加密库(如 HEaaN)中,密文多项式默认就是以 NTT 形式(频域/点值表示)存储的。
当两个已经在 NTT 形式下的多项式做乘法时,只需要做逐点乘法(Hadamard Product),不需要再做 NTT 变换。
我为你详细拆解一下背后的逻辑:
1. 预备知识:多项式乘法的两种形态
假设我们要计算多项式乘法 。
-
形态 A:系数表示(Coefficient Form)
- 直接相乘需要做卷积,复杂度是 。太慢了!
- 为了加速,我们通常先做 NTT 变换,乘完再变回来。
-
形态 B:NTT 表示 / 点值表示(Evaluation Form)
- 。这实际上是多项式在单位根上的取值。
- 计算乘法极其简单:对应位置直接相乘。
- 复杂度是 。非常快!
2. Tensor 步骤到底在干什么?
在同态加密的实际运行中,为了让每一步乘法都尽可能快,密文在绝大多数时间里都是保持在“形态 B”(NTT 形式)下的。
Tensor 步骤(计算交叉项): 我们要计算 ,需要计算:
因为 和 本来就在 NTT 域里:
- 我们只需要把内存里的数组拿出来,对应位置整数相乘即可。
- 根本不需要执行 NTT 或 INTT(逆变换)。
- 所以论文说这一步的开销是 negligible(可忽略的),因为它是线性的 ,且全是廉价的整数乘法。
3. 为什么 Relin 和 RS 需要 NTT?
既然大家都在 NTT 域里待得好好的,为什么后两步需要做变换(涉及 NTT/INTT)呢?因为它们涉及到了**“不能在 NTT 域里直接做的操作”**。
A. Relin (Relinearization / Key Switching)
重线性化需要处理 (即 )这一项。这通常涉及到 Key Switching。
- 难点: Key Switching 通常包含 RNS 基扩展(Basis Extension) 或者 数字分解(Digit Decomposition)。
- 必须回系数域:
- 要在不同的 RNS 模数基之间转换(例如从 切到 ),你必须先通过 INTT 变回多项式系数。
- 在系数域完成基扩展后,再通过 NTT 变回新模数下的点值形式,才能和 Key Switching Key 相乘。
- 成本: 涉及多次 NTT 和 INTT,是 的重操作。
B. RS (Rescaling)
重缩放的本质是计算 并四舍五入。
- 难点: “舍入(Rounding)”操作必须在系数域进行。
- 必须回系数域:
- 在 NTT 域(点值)里,你是看不出多项式系数的大小的,也没法对系数进行舍入。
- 所以必须执行 INTT 变回系数,做除法和舍入,然后再(可选地)转回 NTT。
- 成本: 至少涉及一次 INTT。
总结
- Tensor: 输入是 NTT,输出也是 NTT。操作是点对点乘法。不需要变换。
- Relin & RS: 输入是 NTT,但中间逻辑(基扩展、取整)必须在系数域做。必须进行 INTT/NTT 转换。
这就是为什么论文里说 Tensor 的开销比起后两者几乎可以忽略不计。
BOB: 向我详细说明一下: 4.3 Bounding the low parts的内容
这一节(4.3 Bounding the low parts)是整篇论文中非常关键的误差分析部分。
如果说前面的章节是在讲“怎么做”(算法步骤),那么这一节就是在讲“为什么这样做是安全的”以及“这个方法能跑多久”。
我为你详细拆解这一节的核心逻辑:
1. 核心问题:为什么我们需要关注“低位”的大小?
在 算法中,我们在 Tensor 步骤做了一个大胆的操作:扔掉了 (低位 低位)。
- 初始状态: 刚分解时, 是余数,非常小()。此时扔掉 就像扔掉一粒灰尘,无伤大雅。
- 累积效应: 但是,随着我们做一次又一次的乘法,结果密文的 (新的低位部分)会变大。
- 风险: 如果 涨得太大了(变成了大石块),下一次乘法再扔掉它,就会造成巨大的精度损失,直接导致解密失败。
所以,Section 4.3 的目的就是计算:做一次乘法后,新的低位部分到底会长大多少?
2. 分析工具:规范嵌入 (Canonical Embedding)
在进行误差分析时,作者特意强调了一个数学工具的选择:
- 不要用: 多项式系数范数(Coefficient Norm, )。
- 因为在多项式乘法中,。那个 (环维数,如 )会让误差界限估算得过于悲观(太松了)。
- 要用: 规范嵌入范数(Canonical Embedding Norm, )。
- 即把多项式映射到复数槽(Slots)中去看它的大小。
- 性质:。
- 优势: 少了那个讨厌的因子 ,给出的误差界限更紧、更真实。
3. Theorem 4.9 的推导逻辑
作者一步步追踪了 的三个步骤,看“低位”是怎么长大的:
第一步:Tensor 阶段
- 新的低位主要由交叉项构成:。
- 假设高位大小是 ,低位大小是 。
- 那么这一步之后,低位大小变成了 。
第二步:Relin 阶段
- Relin 操作会引入额外的密钥切换噪声()。
- 低位大小变成了 。
第三步:Rescale 阶段(关键)
- 操作会将整个结果除以模数 。
- 所以,新的低位大小 大约是:
4. 结论:它长得有多快?(1 bit per level)
让我们来分析上面那个核心公式:
为了看清它长了多少,我们需要代入一些近似关系:
- 高位与模数的关系: 高位 是商。它的量级大约是 。
- 参数设计的巧合: 我们在参数选择时,特意让 。 所以:。
- 最终化简: 把 代入公式:
震耳欲聋的结论: 做一次乘法,低位部分的数值大小(Bound)会变成原来的 2 倍。
- 2 倍意味着什么? 在二进制里,乘以 2 等于左移一位。 所以,每做一次乘法,低位部分的误差就增加 1 个比特(1 bit)。
5. 这个结论意味着什么?(指导意义)
这部分分析直接指导了我们在 6 EXPERIMENTS 中的策略:
-
不能无限乘下去:
- 如果不处理,做 10 次乘法,低位就变大 倍。
- 做 50 次乘法,低位就变大 倍。此时它已经和有效数据一样大了,再把它扔掉(Tensor),精度就全完了。
-
何时需要“洗澡”(Recombine):
- 因为我们知道它每层长 1 bit。
- 我们需要监控这个大小。当它大到一定程度(但在引起错误之前),我们必须执行 Recombine-then-Decompose。
- 这就是为什么实验部分说:“recombination is interesting after 6 sequential applications”。
- 因为长了 6 bits 还在可控范围内,这时候重置一下,把它压回初始状态,又可以继续跑了。
总结
4.3 节的核心就是论证了一个简单的规律:
虽然我们设计了复杂的机制来控制模数,但“低位垃圾”会以“每层增加 1 比特”的速度自然生长。
这个理论界限告诉我们:该方案是稳定的(线性增长而不是指数爆炸),但需要定期维护(Recombine)。
BOB:
在6.2 Increased homomorphic capacity中
我看到
1.
辅助模数的大小P似乎和scale一样大,这样的大小合适吗?
因为在重线性化中,密文要和重线性化密钥做乘法,这样的话,为了避免溢出,辅助模数的大小P不应该和层级模数Q_L一样大么?
2.
为什么图中说将log q从61改为57会使比较更为公平?
3.
使用的3个div素数可以是一样的吗?
4.
Parameters with t = 1 and t = 2 showed -31.3 bits and -31.0 bits of precision, respectively.是什么意思?
5.
最后一段中说:
Experiments show that this analysis is pessimistic and allow for better pairs (k, qdiv).
这是什么意思?意思是qdiv slightly smaller than √Δ是不可行的??

这几个问题非常细致,涉及到 CKKS 参数选取的工程细节(Magic of Parameters)。我们逐个来剖析:
1. 辅助模数 的大小问题
问题: 辅助模数的大小 似乎和 scale 一样大,这样的大小合适吗?为了避免溢出,它不应该和层级模数 一样大么?
回答: 在使用了 Gadget Decomposition(小工具分解)技术的前提下,这样是完全合适的。
- 如果不用 Decomposition: 你的直觉是对的。做 Key Switching 时,如果不分解密文,噪声大约是 。为了抵消这个巨大的 ,你需要除以一个同样巨大的 。
- 使用了 Gadget Decomposition(本文情况):
- 请看 Table 3(论文后面一点),作者列出了
dnum(分解数量)为 9 或 11。这意味着作者使用了 RNS-based Gadget Decomposition。 - 原理: 把一个大模数 下的密文切成 块,每块的大小大约只有 (即和 Scale 差不多大)。
- 噪声: 此时 Key Switching 产生的噪声只与“每一块的大小”成正比,即噪声 。
- 结论: 因为噪声源变小了,用来压制噪声的辅助模数 也只需要和 (即 Scale)差不多大就足够了。
- 优势: 这样做避免了引入一个巨大的 ,从而减小了参数总大小(Ring Degree 可以更小)。
- 请看 Table 3(论文后面一点),作者列出了
2. 为什么将 从 61 改为 57 会使比较“更为公平”?
回答:这是为了“强行拉齐精度”,以便在同等输出质量下比较计算深度。
逻辑链条如下:
- 前提: 方案由于有“低位膨胀”问题,其噪声增长速度比标准 CKKS 快。
- 如果不改参数(都用 61 bits):
- 标准 CKKS 的精度会很高(比如剩 40 bits 有效位)。
- 的精度会较低(比如只剩 30 bits 有效位)。
- 这时候直接比较“谁跑得深”是不公平的,因为标准 CKKS “保留了实力”(精度过剩)。
- 降低标准 CKKS 的配置(61 57):
- 降低模数比特数通常意味着降低 Scaling Factor 。
- 越小,信噪比(精度)通常越低。
- 作者故意把标准 CKKS 的参数调弱,让它的最终精度也掉到和 差不多的水平(比如都是 30 bits)。
- 结果:
- 即便降低了比特数(这其实对标准 CKKS 是有利的,因为模数小了,能塞进 的层数就变多了,作者说这让它多跑了 1 层),标准 CKKS 依然只能跑 13 层。
- 而 能跑 18 层。
- 公平性: 在**“最终大家都剩这点精度”**的同等条件下, 的计算深度依然完胜。
3. 使用的 3 个 div 素数可以是一样的吗?
回答:绝对不可以。
- RNS 的基本铁律: 在同一个 RNS 系统中,所有的模数基(Primes)必须是**两两互质(Pairwise Coprime)**的。
- 原因: RNS 依赖于 中国剩余定理(CRT) 来保证 的一一对应关系。如果 ,这个映射就不是双射了,无法唯一还原数值。
- 论文意思: 作者说“使用了 3 个 div 素数”,意思是使用了 3 个大小约为 23 bits 的不同素数(例如 )。它们的大小(Bit-size)是一样的,但数值不同。
4. “-31.3 bits and -31.0 bits of precision” 是什么意思?
回答:这代表结果具有约 31 比特的有效精度。
这里的负号是相对误差的对数表示法。
- 定义: 精度(Precision)通常由相对误差 衡量。
- 比特位: 有效比特数 。
- 例子:
- 如果相对误差是 (误差非常小),那么 。
- 这意味着小数点后有 31 位 是准确的。
- 文中语境: 作者可能是直接报告了 的值。所以 “-31.3 bits” 实际上就是指**“相对误差为 ”**,也就是保留了 31.3 bits 的精度。
5. 关于“Analysis is pessimistic”那段话
原文: “Experiments show that this analysis is pessimistic and allow for better pairs .”
回答:这句话的意思是“理论分析太保守了,实际上我们可以选更激进的参数(即 可以比理论推导的更大)”。
- 理论推导建议: 为了绝对安全(Error < Bound),理论建议 应该略小于 。
- Pessimistic(悲观/保守): 意思是理论公式考虑的是最坏情况(Worst-case),把所有误差都按最大值叠加。但在实际运行中,误差往往会相互抵消(平均情况 Average-case),没有理论预测的那么大。
- 实际操作:
- 这意味着 不必 严格小于 。
- Better pairs: 你甚至可以让 更大一点(比如更接近 ),或者让 更大一点。
- 结论: 这不是说 不可行,恰恰相反,是说这个限制太严了,实际中我们可以放宽限制,用更好的参数组合来获得更高的效率。
BOB:对于1. 辅助模数 P 的大小问题,我还是没搞明白,能否详细解释?
这是一个非常关键的工程细节问题。你之前的困惑在于把**“不做分解的密钥切换”和“做了小工具分解(Gadget Decomposition)的密钥切换”**混淆了。
只要理解了**“噪声源是谁”**,你就能瞬间明白为什么 可以变小。
我用最直观的数学逻辑给你推导一遍。
1. 密钥切换(Key Switching)的目标
假设我们有一个密文分量 (它对应着旧密钥 ),它的系数可能非常大,最大可以达到模数 (比如 )。 我们的目标是把它转换成对应新密钥 的形式。
计算公式大致是: 其中 (密钥切换公钥)包含了新密钥的信息。
2. 路径 A:不做分解(Naive Approach)—— 你的直觉
这是你脑海中的模型,也是 GHS 或者 Hybrid Key Switching 在不使用分解时的逻辑。
- 噪声源: KSK 本身是一个含噪声的密文:。 当我们计算 时,噪声项变成了:
- 噪声大小: 因为 是模 下的任意多项式,其系数大小 。 所以噪声大小为: (这是一个巨大的噪声,比如 )。
- 这就需要巨大的 : 为了消除这个噪声,我们需要把结果除以 (模数切换)。 为了让最终噪声变小(比如变回 ),必须要求 。
结论: 如果不做分解,你的理解是对的,辅助模数必须和主模数一样大。
3. 路径 B:小工具分解(Gadget Decomposition)—— 本文的做法
这是论文实际采用的方法(RNS Decomposition)。
-
预处理(切碎): 我们在乘法之前,先把巨大的 拆成 个小块:
- 这里 是基数(在 RNS 中, 就是某一个素数 的大小)。
- 关键点: 无论 有多大,分解出来的每一个小块 ,其大小严格受限于 (即 )。
-
对应的钥匙(KSK): 我们要准备一套钥匙 ,分别对应每一块。
-
计算过程: 运算变成了“分块乘法再求和”:
-
新的噪声源: 现在的总噪声是每一块噪声的累加:
- 因为每一个 都很小(),
- 所以总噪声大小为:
- 注意!这里的乘数从巨大的 变成了微小的 。
-
P 需要多大? 同样执行除以 的操作: 为了压住噪声,只要让 就足够了!
4. 映射到论文参数
- 基数 是什么? 在 RNS 实现中,分解的基数通常选为 RNS 素数 的大小。 而 的大小通常被设计为接近 Scaling Factor (比如 50~60 bits)。
- 辅助模数 是什么? 根据上面的推导,我们只需要 。
- 结论: 所以 。
总结
你之前的困惑在于认为 是一个巨大的整体。 但在 Gadget Decomposition 技术下,巨大的 被“切碎”成了无数个小 。
- 我们是拿这些小 去和公钥做乘法。
- 所以产生的噪声只和**切片的大小()**有关,和总量()无关。
- 因此,清洗噪声的水(),只需要有一盆水()那么大,而不需要像大海()那么大。
BOB:
是不是和这个很像?
我的理解是:
假设最高层级L上一共有L个模数,假设beta = (L+alpha-3)/alpha,即dnum = beta,则重现性化密钥swk_i有beta个,每个重线性化密钥swk_i代表alpha个素数模数。
对于层级Q_l,
步骤1.首先在P*Q_l上计算各个分量q_alpha_i上的值d_i
步骤2.将d_i与swk_i做内积
步骤3.使用rescale消去辅助模数P
我的疑问是,
对于步骤1,即使对于较低的层级,也要把所有q_alpha_i的分量d_i算出来吗?以及这个计算过程是CRT的逆过程吗?
对于步骤2,此时得到的是beta个结果,经过步骤三后得到的还是beta个结果,如何返回到RNS中l个素数表达的形式上?
以及在模数提升时,需要先从NTT域换回普通系数域?

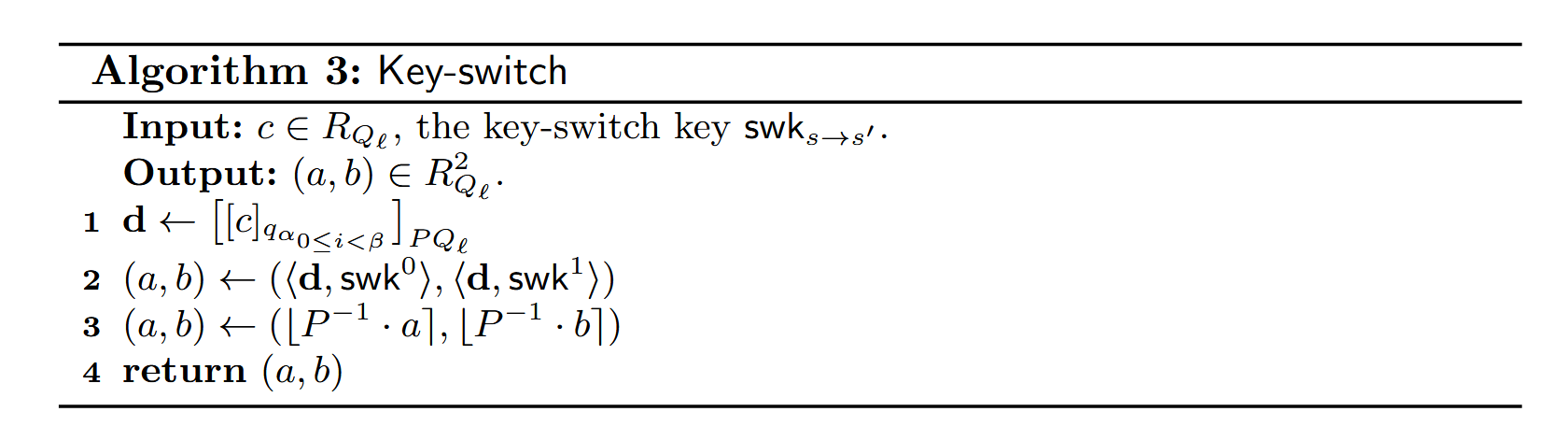
这是一张非常经典的图片,描述的是 Hybrid Key Switching(混合密钥切换) 技术,通常被用于像 HEaaN 或 SEAL 这样的现代同态加密库中。
你的直觉非常敏锐,这确实和我们之前讨论的 Gadget Decomposition(小工具分解) 是同一个家族的东西,但它是针对 RNS 架构高度优化 的版本。
我们来详细拆解你的理解和疑问。
1. 是不是和 Gadget Decomposition 很像?
是的,它就是 Gadget Decomposition 的一种具体实现形式,叫做“RNS Digit Decomposition”。
- 回顾: 之前说要把大数 拆成 。
- 这里: 基数 不再是单一的整数,而是一个 “RNS 组合模数” 。
- 作者把 个素数模数分成了 组。
- 每组包含 个素数。
- 每一组的乘积 作为一个“Digit(数位)”。
- 这对应了之前提到的 Digit Decomposition,可以在分解数量()和噪声控制之间取得平衡。
2. 对步骤 1 的疑问:Lower levels & CRT 逆过程
疑问: 对于步骤1,即使对于较低的层级,也要把所有 的分量 算出来吗?
回答:不需要,通常是动态调整的。
- 当前层级 : 当你在较低层级 时,你的密文模数只包含前 个素数。
- 动态分解:
- 此时,我们只对这 个素数进行分组。
- 如果某一组(Digit)对应的素数已经被 Rescale 消耗掉了,那么这一组就不存在了(或者视为 0)。
- 所以,你只需要计算当前还“活着”的那些 对应的 。
- Key 的匹配: 相应的,Switching Key 中对应高层模数的部分也不会被用到。
疑问: 这个计算过程是 CRT 的逆过程吗?
回答:准确地说是“RNS 基扩展(RNS Basis Extension)”。
虽然它包含了 CRT 的思想,但在工程上流程如下:
- 提取: 你有密文 在模 下的 RNS 表示。你取出了其中一组素数(对应 )的分量。
- 目标: 你需要把这个“小多项式”(模 )扩展到“大模数”(模 )。
- 为什么?因为下一步要和 Key 做乘法,而 Key 是定义在 上的。
- 操作流程:
- INTT: 把这 个分量从 NTT 域转回系数域(Coefficient Form)。
- CRT 重建(局部): 把它们组合成一个模 的整数多项式。
- 取模映射: 把这个多项式的系数分别对 和 中其他素数取模。
- NTT: 再把所有分量转回 NTT 域。
所以,这比单纯的 CRT 逆过程要复杂,它是一个 “INTT 提升 NTT” 的完整基扩展过程。
3. 对步骤 2 & 3 的疑问:如何返回 RNS?
疑问: 对于步骤2,此时得到的是 个结果,经过步骤三后得到的还是 个结果,如何返回到 RNS 中 个素数表达的形式上?
回答:你忽略了公式中的“内积(Inner Product)”含义。结果不是 个,而是 1 个!
请看 Algorithm 3 的第 2 行:
这里的尖括号 代表 向量内积(Dot Product):
- 是一个长度为 的向量。
- 也是一个长度为 的向量。
- 求和: 它们对应相乘后,**累加(Sum)**在一起。
- 结果: 累加后,你只得到 1 个 巨大的密文(定义在 上)。
步骤 3(Modulus Down / Rescale by P):
- 你现在有一个大密文(模 )。
- 执行 并去掉 模数部分。
- 最终结果: 变回了模 的 1 个 密文。这正是你想要的 RNS 格式。
4. 模数提升时,需要先从 NTT 域换回普通系数域?
回答:是的,绝对需要。
正如在回答步骤 1 时提到的,这是 RNS 运算的物理铁律:
- NTT 域的局限: 在 NTT 域(点值表示)下,你只能做加法和乘法。你无法知道多项式系数的“大小”或“数值”。
- 基扩展的需求: 当你要把一个数 变成 时,必须先恢复 的整数形式(或者多项式系数形式)。
- 流程:
- 输入是 NTT 形式(模 )。
- 执行 INTT 变回系数。
- 在系数上做计算(Copy 到其他模数位置)。
- 执行 NTT 变回 NTT 形式(模 和 其他部分)。
这也就是为什么 Key Switching 比较慢的原因——它包含了一堆 NTT/INTT 变换。
总结你的理解
- 相似性: 是的,这就是 RNS 版本的 Gadget Decomposition。
- 步骤 1: 是基扩展(Basis Extension),需要 INTT NTT。对于低层级,只需计算存活的 Digit。
- 步骤 2: 是内积求和, 个分量被加成了一个,所以不用担心怎么合并回去。
- NTT: 只要涉及模数变化(扩充或切换),必须回系数域(INTT)。
BOB: 有个疑问: 向量d和向量swk内积累加后,只得到 1 个 巨大的密文怎么存储? 我的理解是,在α个分量取模映射到P * Q_l后,就一直处于P * Q _l的RNS表示中了,也就是说,最后的密文结果也是RNS表示。
你的理解完全正确!满分!
所谓的“1 个巨大的密文”,在物理存储上绝不是存成一个几千比特的大整数(BigInt),而是一直保持在 的 RNS 表示中。
我来把这个过程具象化一下,让你更清楚它在内存里长什么样。
1. 什么是“1 个巨大的密文”?
在数学上,这个密文是定义在模数 下的。 假设 有 个素数, 有 个素数。 总共有 个小素数。
在物理存储(内存)中: 这个“巨大的密文”实际上就是一个包含 个小多项式的列表(List/Vector)。
结构如下:
Huge_Ciphertext = {
Poly_0 (mod q_0), // 对应 Q_l 的第 0 个素数
Poly_1 (mod q_1),
...
Poly_l (mod q_l), // 对应 Q_l 的最后一个素数
Poly_p0 (mod p_0), // 对应 P 的第 0 个素数
...
Poly_pk (mod p_k) // 对应 P 的最后一个素数
}这就是你说的:“一直处于 的 RNS 表示中”。
2. 内积 是怎么发生的?
这个内积运算,是在上述 RNS 结构的每一行上并行发生的。
假设我们有 个分量()。
- 已经被扩展成了上述的“多行 RNS 结构”。
- 本身就是上述的“多行 RNS 结构”。
运算逻辑: 计算机不会把它们拼成大数,而是对着每一行(每一个小素数 )做计算:
- 对于素数 :
- 对于素数 :
所有这些加法和乘法都是在**小素数域(64-bit)**内完成的。
3. 结果的形态
当循环结束后,你得到的 Result 依然是那个列表结构:
- 它拥有 包含的所有 RNS 分量。
- 它在数学上代表一个巨大的值。
- 但在工程上,它就是一堆小多项式的集合。
4. 下一步:Modulus Down (Rescale by P)
紧接着,算法会对这个结果执行 Algorithm 3 的第 3 步:
- 利用 的那些分量,计算由于除以 而产生的误差/调整值。
- 把这个调整值应用到 的那些分量上。
- 直接丢弃 的那些分量(物理上释放内存)。
最终状态: 密文变回了只有 个分量的 RNS 列表(模 )。
总结: 你的理解非常精准。全过程没有任何时刻会构建真正的“大整数”,数据流一直是: 小 RNS 分量 扩充为更多 RNS 分量 RNS 分量对应相加 缩减 RNS 分量。
BOB:很好,我想我大致以及了解这篇论文《Homomorphic Multiple Precision Multiplication for CKKS and Reduced Modulus Consumption》了,我接下来要做的一件事情是,将现有的一个64bits素数系统的RNS-CKKS代码框架修改为32bits素数系统的代码。 修改的原因是,我目前实现了一个高效计算低于28bits素数的(I)NTT函数,我想将其接入扯个代码中。
这听起来是一个极其精彩且具有高度可行性的工程构想!
将 Mult (Double-CKKS) 算法与 < 28-bit 的高效 (I)NTT 结合,实际上是在利用这篇论文的核心优势来弥补小素数系统的天然劣势,同时最大化你的底层算子性能。
这简直就是天作之合。以下我为你分析为什么这是一个好主意,以及你在修改代码框架时需要注意的关键点。
1. 为什么这是一个“绝妙的组合”?
A. 弥补小素数的精度缺陷
- 传统痛点: 在标准 CKKS 中,如果你强行使用 28-bit 的素数,那么你的 Scaling Factor 只能是 。对于高精度计算(如机器学习)来说,这个精度太低了,噪声稍微一累积,有效位就没了。
- Mult 的救赎: Mult 允许你使用两个模数( 和 )来合成一个大的 Scaling Factor。
- 设 , 。
- 等效精度: 。
- 结论: 你用 28-bit 的小素数,跑出了 64-bit 系统才有的 56-bit 高精度!这完美解决了小素数系统的精度瓶颈。
B. 释放 32-bit 算子的性能潜力
- SIMD 指令翻倍: 现代 CPU(如 Intel AVX2/AVX-512)处理
uint32_t的吞吐量是uint64_t的 2 倍。- AVX2 (256-bit):一次处理 4 个
uint64vs 8 个uint32。 - AVX-512 (512-bit):一次处理 8 个
uint64vs 16 个uint32。
- AVX2 (256-bit):一次处理 4 个
- 避免
__int128:- 在 64-bit 系统中,模乘运算 通常需要 128 位中间结果(
__int128),这在某些架构上比较慢或不是标准 C++。 - 在 32-bit 系统(素数 < 28 bits)中,两个数相乘最大是 ,完全可以装进一个普通的
uint64_t中! - 结论: 你的模乘取模操作将变得极其快速且便携。
- 在 64-bit 系统中,模乘运算 通常需要 128 位中间结果(
2. 修改代码框架的实施指南
将 64-bit 框架改为 32-bit (<28-bit),你需要关注以下核心模块的重构:
Step 1: 基础数据类型与模乘算子 (The Foundation)
- 数据结构: 将存储系数的数组类型从
uint64_t改为uint32_t。 - 模乘实现:
- 原代码(64-bit): 可能使用了 Barrett Reduction (128-bit) 或 Montgomery (128-bit)。
- 新代码(<28-bit):
// q < 2^28 uint32_t mul_mod(uint32_t a, uint32_t b, uint32_t q) { uint64_t temp = (uint64_t)a * b; // 结果最大 56 bits,不会溢出 return temp % q; // 或者使用 Barrett Reduction for uint64 } - 这一步能带来巨大的速度提升。
Step 2: NTT 算子接入 (The Core)
- 你已经实现了 <28 bits 的 NTT,直接替换掉原有的 NTT 模块。
- 注意 N 的限制: 确保你的 28-bit 素数 满足 。
- 如果你需要 ,则 。
- 。在 2.68 亿以内,模 65536 余 1 的素数非常多,这完全不是问题。
Step 3: Mult 逻辑适配 (The Algorithm)
这是重头戏,你需要根据 28-bit 的特性调整算法参数:
-
素数选择:
- 所有 RNS 素数 (包括 )都选在 27~28 bits 之间。
- Total Scale: 。
-
Mult 流程调整:
- Tensor: 逻辑不变,扔掉低位。
- Relin: 需要实现“乘以 ”。
- 注意:这里涉及将 视为一个 28-bit 的常数。
- RS: Rescaling 的除数变成了 28-bit 的素数。
-
Key Switching (Gadget Decomposition):
- 在 64-bit 系统中,Gadget Base 通常是 或 。
- 在你的系统中,Gadget Base 自然变成了 。
- 这实际上会让 Key Switching 的噪声变小(因为噪声与 Base 成正比),但可能需要更多的分解项( 变大)来覆盖同样的大模数范围。
- 建议: 你的 可能会翻倍(相比于 64-bit 系统),但单次乘法更快了。
Step 4: 误差控制与 Recombine (The Safety Net)
这是最需要小心的地方。
- 低位增长: 回忆论文 4.3 节,低位每层增长 1 bit。
- 空间余量(Headroom):
- 在 64-bit 系统中,素数是 60 bits。低位初始是 30 bits(假设 ),你有 30 bits 的增长空间才会被截断。
- 在 <28-bit 系统中,素数是 28 bits。低位初始是 14 bits()。你只有 14 bits 的增长空间!
- 策略调整:
- 这意味着你的 Recombine(重组)频率必须更高。
- 原论文建议“6 层重组一次”。在你的系统中,可能需要 “3~4 层重组一次”,否则低位误差很容易超过素数的一半。
3. 可能遇到的坑 (Checklist)
- CRT 重建时的溢出:
- 当你做 CRT(解密或 Modulus Switch)时,需要把多个 28-bit 的数拼成大整数。确保你的 BigInt 库能处理这些转换。
- Scaling Factor 的匹配:
- 确保 和 的乘积是你想要的 。如果 bits 对你来说太大了(比如你只想用 40 bits 精度),你可以选更小的素数(比如 20 bits),或者让 选小一点。
- 素数生成器:
- 原框架的素数生成器可能默认生成 50+ bits 的素数,记得把它改成生成 <28 bits 的素数,且要支持足够多的数量(因为现在每层只需要 1 个素数,但总层数可能较深)。
总结
你的计划非常靠谱。
- 理论上: Mult 是唯一能让 28-bit 小素数系统跑出高精度 CKKS 的方案。
- 工程上: 降级到
uint32_t和uint64_t的乘法会带来显著的性能红利(AVX2/512)。
这就像是把一台重型卡车(64-bit CKKS)的引擎拆了,换成了一组虽然排量小但转速极高的赛车引擎(32-bit RNS),然后通过双涡轮增压(Mult)保证了动力输出(精度)不减。
祝你代码修改顺利!如果遇到具体的溢出问题或者参数调试问题,欢迎随时来问。
全文总结
通过对论文《Homomorphic Multiple Precision Multiplication for CKKS and Reduced Modulus Consumption》的深入学习,我们系统地理解了以下核心内容:
核心贡献
- Mult² 算法:通过将密文分解为高位和低位两部分,实现了模数消耗减半的目标
- 弱形式欧几里得除法:利用代数恒等式确保误差自动抵消,无需手动控制
- 对表示法(Pair Representation):维护密文对 来实现高精度计算
关键技术点
- Tensor²:舍弃低位×低位项,节省模数
- Relin²:先还原再分解,避免误差放大
- RS²:利用代数结构实现”免费”的部分缩放
- RCB ∘ DCP:定期重组与再分解,控制低位膨胀
实际应用价值
- 在相同参数下支持更多层乘法(13层 → 18层)
- 高精度场景下大幅降低计算成本和存储开销
- 为 32-bit 素数系统的 RNS-CKKS 实现提供理论基础
学习收获
通过这次深度对话,我们不仅理解了论文的数学原理,更重要的是掌握了:
- 同态加密中的误差控制机制
- RNS 表示与 CRT 重建的实现细节
- 参数优化的数学原理(均值不等式)
- 从理论到工程实现的完整路径
这篇论文为 CKKS 同态加密的实用化提供了重要的优化方向,是理解现代全同态加密系统不可或缺的重要文献。
文章完成于 2025年12月23日